Page 2 of 3
Re: DMC energy
Posted: Thu Aug 04, 2016 4:49 pm
by Neil Drummond
P.S. I think the most likely reason for the apparent disagreement in the DMC results with different Jastrows is the need for a better treatment of population-control errors in the no-Jastrow case. I suggest varying the target weight in inverse proportion to the time step.
Re: DMC energy
Posted: Sun Aug 07, 2016 10:58 am
by Katharina Doblhoff
Dear Neil,
the time-step and equilibration times you suggest, seem to be similar to what Fan-Wang used (and he says he checked for the equilibration time). This would leave the population bias as source of error (although I am still not convinced that a linear extrapolation from 0.002 and 0.0006 for the Jastrow-less trial-wavefunction is any good)....
Concerning the orbitals:
even if there were a problem with the gaussian orbitals, this should not lead to a dependence of the DMC energy on the Jastrow factor.
I am now becoming very curious as to what leads to these numbers!
Re: DMC energy
Posted: Tue Aug 16, 2016 4:00 pm
by Mike Towler
Hi Fan,
Did you reach any conclusions with this?
Mike
Re: DMC energy
Posted: Wed Aug 17, 2016 4:19 am
by Fan_Wang
Dear Mike, Neil and Katharina,
Calculations without Jastrow factor is very expensive and I only have limited computational resources. I have the following feelings about DMC calculations from my experience (also some of my students) on a bunch of molecules and atoms:
(1) Population size or target weight has almost no effect on results. (I am currently using 2048 walkers.) I tried 8192 walkers and difference in total energy is only 0.0001 a.u.
This is something I do not understand. Why increasing population size will reduce population-control bias? I found one of Neil's talk slide and it mentioned that population control bias decreased as 1/M.
(2) Generally I do not trust extrapolation, although we have to live with it in QMC. You can easily get a total energy difference of more than 1kcal/mol using linear fitting or quadratic fitting.
The way I prefer is to include a small time-step result in extrapolation and to use quadratic fitting. I also need to check that the extrapolated results are not very far from small time-step results.
I do not think there exists some "linear regime" except that you use rather large time step, at least for the molecules and atoms I am investigating. I generally do not trust results from extrapolation using large time-steps.
IN PRACTICE, how you do extrapolation may be not so important, since we ONLY concerns about energy difference and we ALWAYS rely on error cancellation.
(3) As for all-electron DMC energy using Slater-Jastrow and Slater determinant as trial wavefunction, difference for C is negligible. However, you can still see some difference for N, ~0.0006(2) a.u., while it even larger for O, as I showed you. I do not think this is something wrong with my calculations. It is probably what it is in practical implementation of DMC. Right now, I suspect this may be due to the modification of Green's function near nucleus. I may try it.
(4) I have to learn to live with some kind of uncertainties. In my implementation for coupled-cluster code, a difference of 10^-5a.u. means these is something wrong with your code. However, when you see a difference of something like 0.0003(1)a.u. in QMC, I really do not know whether this difference is meaningful.
I tried VMC for oxygen with Hartree-Fock Slater determinant and turned off the cusp-correction, I got -74.8064(15), while the Hartree-Fock energy is -74.80806. It SEEMS the results are OK.
with best regards,
Fan
Re: DMC energy
Posted: Sun Jun 11, 2017 12:18 pm
by Vladimir_Konjkov
Hello all.
I'm going to do the all-electrons calculations of DMC energy of for a set of about 150 molecules сonsisting of atoms from H up to Cl.
After obtaining initial molecular orbitals (from ORCA and QCHEM) and performing some JASTROW optimization, I decided to compare how much DMC energy depends on the JASTROW.
In my test case, calculations were made for an aluminum atom and I used three different ways to optimize JASTROW:
1. Only [2.0] and [1,1] terms of 8 order both, emin optimized.
2. [2.0] and [1,1] terms of 8 order both and [2,1] term of 4 e-e order and 4 e-n order, emin optimized.
3. same as 2. but madmin optimized.
I have got different DMC energies in all cases:
1.
[del]DMC time step = 0.001; 3072 configurations; Total energy = -242.3179(4)[/del]
DMC time step = 0.003; 1024 configurations; Total energy = -242.3178(4)
2.
DMC time step = 0.001; 3072 configurations; Total energy = -242.3216(3)
DMC time step = 0.003; 1024 configurations; Total energy = -242.3216(3)
3.
DMC time step = 0.001; 3072 configurations; Total energy = -242.3218(3)
DMC time step = 0.003; 1024 configurations; Total energy = -242.3239(3)
time-step bais and population control bias are insignificant in first and second cases but the energy differs significantly.
Are there any assumptions about the reason for this discrepancy?
In the near future, I will attach the results of calculations in the form of file archives.
Re: DMC energy
Posted: Sun Jun 11, 2017 9:24 pm
by Neil Drummond
Dear Vladimir,
[b]All-electron DMC calculations with different Jastrow factors ought to agree exactly (within statistical error bars) in the limit of zero time step, infinite population and with an adequate equilibration period...[/b]
For an aluminium atom (Z=13) the Bohr radius is 1/13 a.u., suggesting the time step tau should satisfy sqrt(3.tau) << 1/13, i.e., tau << 0.002 a.u to be in the linear bias regime. The size of the atom is ~ 2 a.u., so that the number of equilibration steps N_eq should be sqrt(3.tau.N_eq) >> 2, i.e., N_eq >> 4/(3.tau). The Kato cusp conditions should be imposed on the wave function.
I would use time steps of 0.001 a.u. and 0.0005 a.u.; populations of 1024 and 4096 configurations, respectively; and 20,000 equilibration steps.
Best wishes,
Neil.
Re: DMC energy
Posted: Mon Jun 12, 2017 2:01 am
by Vladimir_Konjkov
Neil Drummond wrote:Dear Vladimir,
All-electron DMC calculations with different Jastrow factors ought to agree exactly (within statistical error bars) in the limit of zero time step, infinite population and with an adequate equilibration period...
For an aluminium atom (Z=13) the Bohr radius is 1/13 a.u., suggesting the time step tau should satisfy sqrt(3.tau) << 1/13, i.e., tau << 0.002 a.u to be in the linear bias regime. The size of the atom is ~ 2 a.u., so that the number of equilibration steps N_eq should be sqrt(3.tau.N_eq) >> 2, i.e., N_eq >> 4/(3.tau). The Kato cusp conditions should be imposed on the wave function.
I would use time steps of 0.001 a.u. and 0.0005 a.u.; populations of 1024 and 4096 configurations, respectively; and 20,000 equilibration steps.
Best wishes,
Neil.
Thank you, Neil for the detailed answer. Which form of JASTROW will be optimal for achieving the desired DMC energy accuracy in the minimum amount of time? At first sight, there is almost no difference between all JASTROW.
And How should I calculate time steps and equilibration steps for сomplex molecule like
Halothane (radius 2.91 A) hypothetically, I will not calculate it.
timestep for single bromine atom should be << (1/35.0)^2/3 = 0.00027 can it be applied for whole molecule?. And what about equilibration steps?
Re: DMC energy
Posted: Mon Jun 12, 2017 8:36 am
by Neil Drummond
Sorry, the time steps should have been 0.001 and 0.00025 a.u. (ratio of 4:1), with populations of 1024 and 4096, respectively (4:1), for optimal efficiency (with twice as many statistics accumulation steps for the smaller time step).
The shortest length scale in an all-electron calculation is the Bohr radius (1/Z) of the largest atom; this determines the time step. The longest relevant length scale (for estimating the number of equilibration steps) is not so easy to estimate, but the physical size of the molecule is an upper bound.
Best wishes,
Neil.
Re: DMC energy
Posted: Tue Jun 13, 2017 6:51 am
by Vladimir_Konjkov
Neil Drummond wrote:Sorry, the time steps should have been 0.001 and 0.00025 a.u. (ratio of 4:1), with populations of 1024 and 4096, respectively (4:1), for optimal efficiency (with twice as many statistics accumulation steps for the smaller time step).
The shortest length scale in an all-electron calculation is the Bohr radius (1/Z) of the largest atom; this determines the time step. The longest relevant length scale (for estimating the number of equilibration steps) is not so easy to estimate, but the physical size of the molecule is an upper bound.
Best wishes,
Neil.
I just remembered a useful article about
improving the efficiency of quantum Monte Carlo calculations. Prof. Towler told me.
Can I use
Optimized vmc_decorr_period from VMC calculation to estimate longest relevant length scale?
Re: DMC energy
Posted: Tue Jun 13, 2017 12:30 pm
by Vladimir_Konjkov
I run 1000 equilibration steps 0.01 au each for Be atom with 102400 configurations, split it to 50 groups and plot it with VMC, DMC energies and fits it with exponential an 1/x decay.
This test takes 1000 sec for me.
1/x decay fiits better, is it bad news?
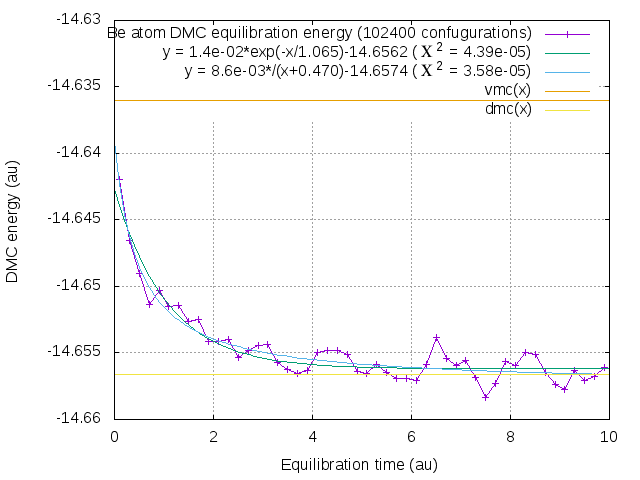
- Equilibration graph
- dmc_equilibration.png (9.85 KiB) Viewed 60145 times
Actually it means that energy vary with the DMC equilibration time as
E(dt) = (DMC * dt + b * VMC)/(dt + b) where b = 0.47 +- 0.09 au
and equilibration bias is:
E(dt)-DMC = b*(VMC-DMC)/dt when dt >> b
UPD
More accurately if you perform EQUILIBRATION CALCULATION t1 (au) long and STATISTICS-ACCUMULATION CALCULATION t2 (au) long and t2 > t1 >> b than we must integrate:
E - DMC ~ b*(VMC-DMC)*ln(1+t2/t1)/t2
