Page 1 of 2
DMC timestep bias asymptotic
Posted: Fri Mar 09, 2018 6:27 am
by Vladimir_Konjkov
Hello everyone who does DMC calculations.
I calculated the time step bias dependence for simple full electron systems like H-Cl atoms and some diatomic.
I've found that small time step asymptotic is rather quadratic than linear whereas large time step asymptotic is linear in some cases.
For example Be atom with 4 determinant WFN which is known to give the correct nodal surface
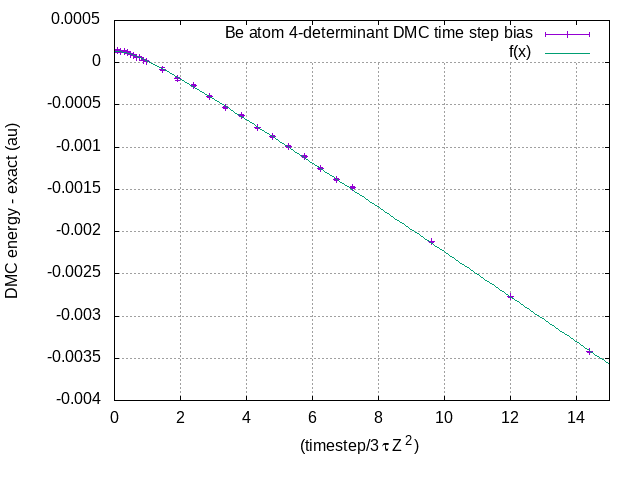
- be_4det.png (7.89 KiB) Viewed 83184 times
For example B atom with 3 determinant WFN which is known to give the correct nodal surface
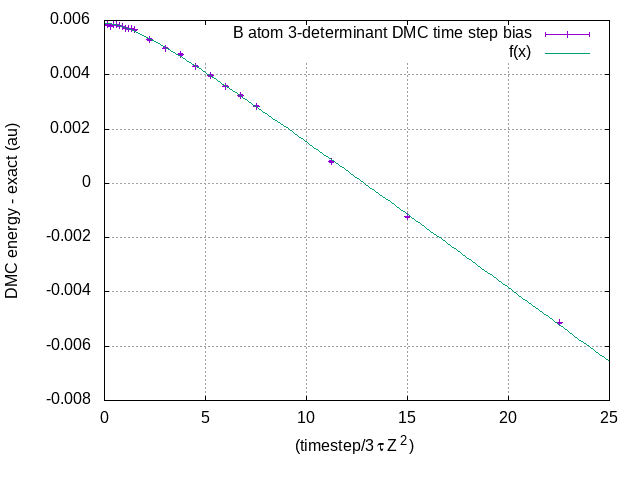
- b_3det.png (7.65 KiB) Viewed 83184 times
For comparition F atom and F2 molecules the slopes match exactly
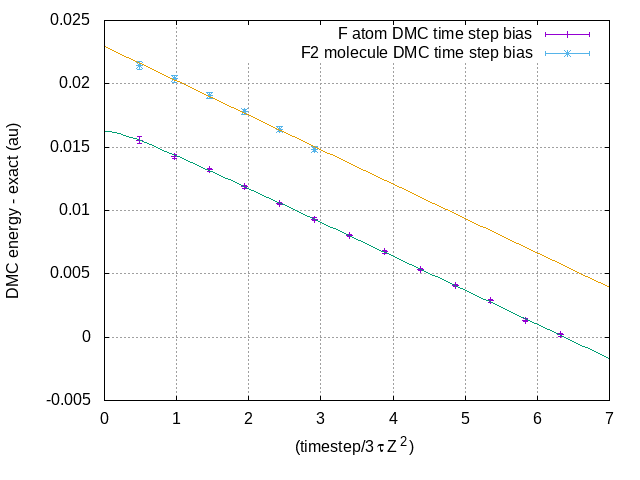
- f_f2.png (8.37 KiB) Viewed 83184 times
As for single determinant Be and B atoms and Be2 molecule which nodal surface is not exact asymptotic is not linear.
So is there any equation which describe DMC time step bias asymptotic behavior arising from different sources of nodal surface non-ideality or the finiteness of the time step itself?
Best Vladimir
Re: DMC timestep bias asymptotic
Posted: Fri Mar 09, 2018 6:43 am
by Cyrus_Umrigar
If you look at Fig. 13 of Umrigar, Nightingale, Runge, J. Chem. Phys. 1993, you will see that it is nearly quadratic near tau=0.
I do not know of a theoretical argument for the behaviour of the time-step error.
What is the x-scale on your plots?
Cyrus
Re: DMC timestep bias asymptotic
Posted: Fri Mar 09, 2018 7:28 am
by Vladimir_Konjkov
Cyrus_Umrigar wrote:If you look at Fig. 13 of Umrigar, Nightingale, Runge, J. Chem. Phys. 1993, you will see that it is nearly quadratic near tau=0.
I do not know of a theoretical argument for the behaviour of the time-step error.
What is the x-scale on your plots?
Cyrus
X scale is time step divided by τ = 1/(3Z^2), where Z is the largest atomic number occurring in the system. As described in the
Phys Rev E Stat Nonlin Soft Matter Phys. 2012 Feb;85(2 Pt 2):029908. DOI: 10.1103/PhysRevE.83.066706
For all-electron atomic systems, one would expect the linear regime to occur for time steps less than of the order τ.
I think there is a hint for DMC time step bias cancellation in the TAE calculation, this is good news since computing with a small time step very resource demanding as DMC data correlated.
Best Vladimir.
Re: DMC timestep bias asymptotic
Posted: Fri Mar 09, 2018 8:17 am
by Vladimir_Konjkov
Hello Cyrus
I just read the article and want to note that in the case of single determinant WFN for Be atom and Be2 molecule which are known to give the wrong topology of nodal surface DMC time step bias no longer linear
I applied polynomial interpolation
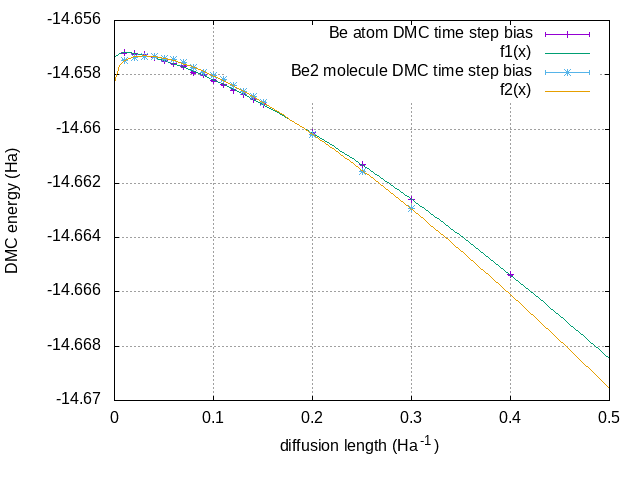
- be_be2.png (9.16 KiB) Viewed 83157 times
E(Be) = -0.022459*x^1.5 - 0.0104496*x + 0.00290101*x^0.5 - 14.6573
E(Be2 + TAE)/2 = -0.0164055*x^1.5 - 0.0259155*x + 0.0105734*x^0.5 - 14.6583
TAE = 0.00424 (Total energy atomization Be2 from
J. Phys. Chem. A, 2008, 112 (50), pp 12868–12886 DOI: 10.1021/jp801805p (TABLE 2 / TAEe^a) )
I think that the unexactness of the nodal surface contributes to the time step bias greatly in case of single determinant Be and Be2. In other hand time step bias exists even when nodal surface is exact (H, He, Li atoms) what can cause it in this case?
Best, Vladimir.
Re: DMC timestep bias asymptotic
Posted: Fri Mar 09, 2018 11:48 am
by Neil Drummond
Dear Vladimir,
One argument for the time-step bias in the energy being linear is that the time-step error in the DMC Green's function is O(tau^2), and hence time-step errors are introduced at a rate O(tau^2)/tau=O(tau) into the mixed wave function f(R,t)=phi(R,t).Psi(R), where Psi(R) is the trial wave function and phi(R,t) is the solution of the imaginary-time Schroedinger equation. At the same time, the DMC algorithm is driving f exponentially towards the ground state phi_0(R).Psi(R), where phi_0 is the fixed-node ground state wave function, at a rate given by the correlation time T_corr. Hence the error Delta f in the mixed wave function is being removed at a rate Delta f / T_corr. In equilibrium the rates at which errors are introduced and removed from f balance, and so Delta f is proportional to the time step tau. The error in f then carries over to other expectation values, including the energy, giving a linear bias.
In this case, could there be some sort of issue with the Gaussian basis set (or perhaps even with the treatment of the nodal surface in the multideterminant wave function) that introduces a new, small length scale into the problem, resulting in a crossover between two different linear bias regimes?
Best wishes,
Neil.
Re: DMC timestep bias asymptotic
Posted: Fri Mar 09, 2018 3:51 pm
by Vladimir_Konjkov
Thanks Neil for the detailed explanation.
Сan you from such simple reasoning predict the sign of time step bias? Suppose that nodal surface is exact but trial WFN isn't.
As you can see from my plots time step error has negative sign.
Best Vladimir.
Re: DMC timestep bias asymptotic
Posted: Fri Mar 09, 2018 4:16 pm
by Neil Drummond
The errors in the DMC Green's function, in f(R) and hence in the energy can be of either sign. In my experience time-step bias in the energy is usually, but not always, positive.
Best wishes,
Neil.
Re: DMC timestep bias asymptotic
Posted: Fri Mar 16, 2018 5:14 am
by Vladimir_Konjkov
Neil Drummond wrote:Dear Vladimir,
One argument for the time-step bias in the energy being linear is that the time-step error in the DMC Green's function is O(tau^2), and hence time-step errors are introduced at a rate O(tau^2)/tau=O(tau) into the mixed wave function f(R,t)=phi(R,t).Psi(R), where Psi(R) is the trial wave function and phi(R,t) is the solution of the imaginary-time Schroedinger equation. At the same time, the DMC algorithm is driving f exponentially towards the ground state phi_0(R).Psi(R), where phi_0 is the fixed-node ground state wave function, at a rate given by the correlation time T_corr. Hence the error Delta f in the mixed wave function is being removed at a rate Delta f / T_corr. In equilibrium the rates at which errors are introduced and removed from f balance, and so Delta f is proportional to the time step tau. The error in f then carries over to other expectation values, including the energy, giving a linear bias.
In this case, could there be some sort of issue with the Gaussian basis set (or perhaps even with the treatment of the nodal surface in the multideterminant wave function) that introduces a new, small length scale into the problem, resulting in a crossover between two different linear bias regimes?
Best wishes,
Neil.
Hello Neil
As I understand, Psi(
R) obeys the e-e and e-n Kato cusp conditions as we set CUSP CORRECTION to TRUE in the input files, but does the phi(
R,
t) have the same properties?
I think that in the case of the zero time step it does, but if we perform the fourier transform of phi_0(
R,
t) and apply low-pass filter (freq lower than 1/tau) than transform back we will get roughly phi(
R,
t).
I think we will break Kato cusp conditions for phi(
R,
t).
Сan we impose Kato cusp conditions for phi(
R,
t) by hands?
Best Vladimir.
Re: DMC timestep bias asymptotic
Posted: Fri Mar 16, 2018 9:44 am
by Neil Drummond
Dear Vladimir,
You are certainly right that the behaviour around nuclei makes a big difference to the finite time-step behaviour. Cyrus Umrigar's modifications to the DMC Green's functions [Umrigar, Nightingale and Runge, JCP 99, 2865, (1993)] impose the cusp-like behaviour around nuclei at finite time step, and they certainly greatly reduce time-step errors. These modifications are used by default in CASINO if bare nuclei are present (switch them off using the nucleus_gf_mods keyword if you want to investigate).
Best wishes,
Neil.
Re: DMC timestep bias asymptotic
Posted: Sat Apr 28, 2018 1:14 am
by Vladimir_Konjkov
Hello Cyrus
I did not immediately notice that in your article the slater bases was used. I tried to use a similar basis from ANO family.
In the ORCA program there is a set of such bases - ano-pVDZ, ano-pVTZ, ano-pVQZ,
https://pubs.acs.org/doi/abs/10.1021/ct100396y for details.
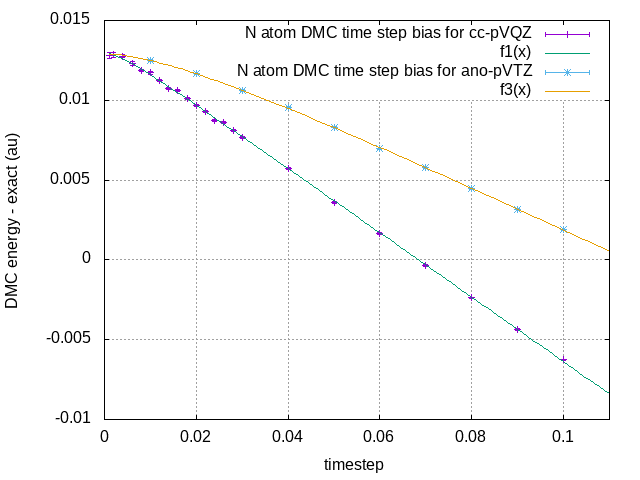
- n atom time step bias
- n.png (8.55 KiB) Viewed 82734 times
It can be seen that the parabolic section has become larger in case of ANO basis (quadratic term is 8 times larger from extrapolation).
This suggests that the time step bias depends on the basis, and especially on the WFN behavior near the nucleus.
It would be very good to transform Gaussian ANO basis to corresponding Slater and use for VMC/DMC calculions.
Qualitatively the graph is similar to the same from the article
https://aip.scitation.org/doi/abs/10.1063/1.2204600 which is marked as “GF mods”
unfortunately from the article I did not understand what basis set was used.