Dear Pablo and Neil.
Thanks for the answers, I just wanted to quote the article of Dario Bressanini "Implications of the two nodal domains conjecture for ground state fermionic wave functions" which stated that the quality of the HF wave function for four electron atoms can be greatly improved by adding 2s2->2p2 double excitation which corresponds to a near-degeneracy effect. The 2-configuration wave function can be obtained using CASSCF(2,4) method and consists of 4 determinants if graphical unitary group approach (GUGA) is used to construct configuration state functions (CSFs).
The nodal set of 2-configuration wave function is completely different from that of HF, independent nodal surfaces of the HF configuration merge, an “opening” appears where the two surfaces previously crossed, and only one hypersurface is left, with only two nodal pokets.
it is shown in the following figure:
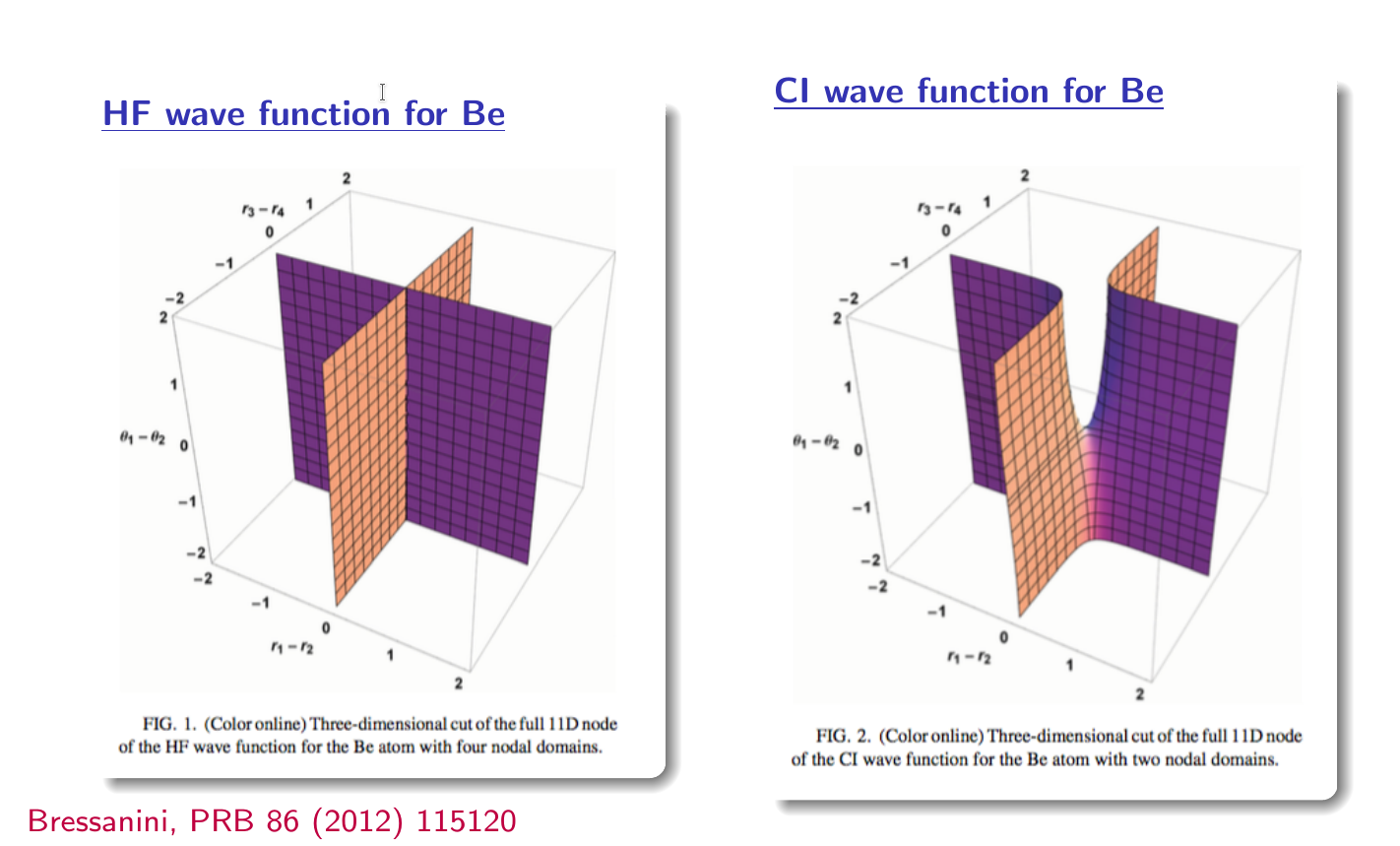
- Bressanini.png (396 KiB) Viewed 62974 times
If we want to get exact nodal surface given HF wave function for the Be atom and backflow transformation, we should transform the points on the right nodal surface using backflow to points on the left nodal surface and substitute these coordinates into HF wave function for the Be atom.
Because HF wave function for the Be atom is equal to zero when the points is on the left surface, but we need when they are on the right.
This should be understood taking into account the fact that the figures show 3-dimensional cuts of a 12-dimensional space and the backflow transforms points of the right cut to set of left cuts, because the coordinates of all electrons are transformed simultaneously. Since these surfaces are not topologically equivalent, it is not possible to transform one into the another using homeomorphism which backflow is. To understand what kind of nodal surface is obtained in the emin/madmin/varmin optimization process, it is necessary to imagine a nodal surface as close as possible to the ideal one (on the right), but topologically equivalent to HF one (on the left), that is, it should have 4 nodal pockets.
I belive that in this case an “opening” appeared in the case of an ideal nodal surface will be closed by a bilayers, but with a long enough dtdmc step the bilayer becomes permeable to walkers. I don`t know whether the angle between two independent nodes remains π/2, this is a consequence of finiteness of local energy -> zero value of the Laplacian of the wave function at the point of intersection of nodes -> if wfn approximate by quadratic form -> angle between two independent nodes = π/2.
But backflow transformation is not conformal mapping so angles are not preserved and it lead me to the conclusion that the backflow creates a far from ideal nodal surface no matter how functionally complex and ideal we make it, inhomogeneous or orbital–dependent both should be equally inaccurate and it turns out that this is so, but I did not finish the calculations.
Yep, this is not the whole my answer I need to think more. But your answers are quite interesting they give me a different point of view on backflow.
Best wishes, Vladimir.
In Soviet Russia Casino plays you.