Magnetic interactions and the co-operative Jahn-Teller effect in KCuF3
Michael Towler and Roberto Dovesi
Gruppo di Chimica Teorica, Dipartimento CIFM, Università di Torino, via P. Giuria 5, I-10125 Torino, Italy
Victor R. Saunders
CCLRC Daresbury Laboratory, Daresbury, Warrington WA4 4AD, U.K.
{appeared in Phys. Rev. B, 52, 10150 (1995)}
Abstract
We have investigated the electronic structure of the Jahn-Teller distorted perovskite KCuF3 using a periodic ab initio unrestricted Hartree-Fock approach. The calculations correctly indicate the ground state to be an orbitally ordered wide band gap insulator with quasi-one-dimensional magnetic properties; our estimated exchange coupling constant Jc suggests an antiferromagnetic interaction along the c axis two orders of magnitude larger than the small ferromagnetic interaction perpendicular to this axis, in spite of the pseudocubic arrangement of magnetic Cu ions in the crystal structure. The adiabatic potential energy surface corresponding to co-operative distortions of the CuF6 octahedra has the form of a classical Jahn-Teller double well with the equilibrium distortion close to that observed experimentally. The interplay between the Jahn-Teller distortion and the superexchange interaction is found to be responsible for the unusual magnetic behaviour.
PACS Numbers: 75.25.+z, 75.30.Et, 75.50.-y, 71.10.+x
Introduction
The perovskite KCuF3 has attracted significant theoretical and experimental interest since the 1960s, principally because it is one of very few pseudocubic materials to exhibit effectively one-dimensional magnetic properties. This behaviour is known to be associated with a rather subtle interaction of exchange effects and 'orbital ordering' stemming from co-operative Jahn-Teller distortions of the CuF6 octahedra that make up the crystal structure. Other similar materials which do not contain Jahn-Teller ions, such as the cubic perovskites KNiF3 and KMnF3, are regular three-dimensional antiferromagnets [1].
While perturbation-theoretical arguments have been successfully used
to explain such phenomena [2], an accurate ab
initio study has yet to be performed. In fact for magnetic insulators
in general the well-known difficulties arising from the self-interaction
error inherent in local density functional methods have generally precluded
calculations of this kind. However, recent studies by us of NiO and other
magnetic insulators [1, 3-5] have suggested that the
periodic spin-unrestricted Hartree-Fock approach might be of some utility
in this field. This is primarily because the Hartree-Fock Hamiltonian contains
the full non-local exchange interaction, which is responsible to first
order for the magnetic properties of transition metal compounds, and which
directly cancels the self-interaction error encountered in local
density functional calculations. The incorrect description of d
orbital polarization effects in the presence of self-interaction errors
usually leads, for example, to the lack of a gap in the band structure
and incorrect relative stabilities of ferromagnetic and antiferromagnetic
states [6]. Furthermore, the numerical accuracy of
our computational implementation of the periodic Hartree-Fock equations
may be made high enough to study total energy differences reliably down
to at least 10-5 Hartree per cell at reasonable
cost. This is particularly useful in the analysis of energy differences
between magnetic states (and hence in the estimation of exchange constants)
which are often of this order of magnitude. In the remainder of this article
we shall therefore present the results of an ab initio periodic
unrestricted Hartree-Fock study of KCuF3.

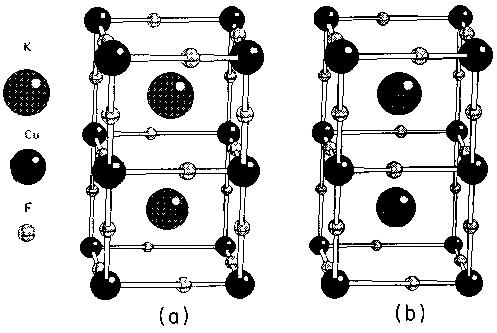
Figure 1 - Tetragonal unit cell of KCuF3, showing the two different polytype structures (a) untwisted, type ‘d’ and (b) twisted, type ‘a’.
The crystal structure of this material (Fig. 1) is made up of an array of CuF6 octahedra that is pseudocubic, in the sense that the distance between magnetic Cu2+ ions is almost the same along all three principal axes. The K+ ions fill the spaces between octahedra. In the planes perpendicular to the c axis, small co-operative Jahn-Teller distortions are observed. Each CuF6 octahedron is slightly elongated along the a or b principal axes such that the distortion is orthogonal to that of neighbouring octahedra in the plane. All F ions in the ab planes are slightly displaced from the midpoint of adjacent Cu sites, whereas the F ions located between these planes occupy symmetric positions. The structure thus contains two distinct fluorine ions which will be denoted by F1 (bond-centred F) and F2 (displaced F). For reasons to be discussed presently, this ‘antiferrodistortive’ behaviour effectively confines the magnetic interactions to isolated linear chains along the c axis; the antiferromagnetic exchange constant Jc in this direction is several orders of magnitude greater than the weakly ferromagnetic exchange constant Ja in the Jahn-Teller disordered plane [35].
It is known that at least two distinct types of polytype structure occur naturally in KCuF3. Apart from in very carefully prepared crystals, these usually coexist in any given sample. In one type [Fig. 1(b)] the direction of displacement of F ions from the midpoint of adjacent Cu sites is opposite in neighbouring ab planes, whereas in the alternative structure the displacements are always in the same sense [Fig. 1(a)]. We shall refer to these as twisted and untwisted polytypes, although for historical reasons the usual designation is type ‘a’ and type ‘d’ [7]. In this paper we shall be principally concerned with the untwisted polytype, which has a smaller unit cell, although total energy comparisons between the two polytypes will be made. There are three independent structural parameters, a, c and the F2 coordinate xF, for which the most recent structural refinements suggest the following values. For the twisted ‘a’ polytype (space group I4/mcm) a = 5.8569 Å, c = 7.8487Å and xF = 0.22803 and for the untwisted ‘d’ polytype (space group P4/mbm), a = 5.8542 Å, c = 3.9303 Å with xF not reported [8]. 2xF (= XF) corresponds to the position of the F2 fluorine ion as a proportion of the length of the Cu-F2-Cu vector (i.e. the undistorted position 0.5 corresponds to xF = 0.25).
The low-temperature experimental spin arrangement consists of strongly antiferromagnetic linear chains along the c-axis coupled via a weakly ferromagnetic interaction. In order to study the magnetic interactions, calculations were performed using the ferromagnetic (F) and two antiferromagnetic states, defined as follows. The state corresponding most closely to the experimental spin arrangement consists of ferromagnetic ab sheets with adjacent sheets having opposite spin. This will be referred to as the AF1 phase. To study the intra-plane exchange interaction, we also define a hypothetical alternative phase (AF2), in which all ab planes are identical, and the nearest-neighbour superexchange contacts within these planes are antiferromagnetic. Other possible spin arrangements with larger unit cells were not considered. The origin of the anisotropic magnetic behaviour in KCuF3 is generally explained as a result of orbital ordering effects associated with the co-operative Jahn-Teller distorted array. The principle component of what one might call the ‘hole orbital’ of Cu2+ is thought to alternate between ‘dx2-z2’ and ‘dy2-z2’ on adjacent Cu sites, a feature of the electron density which has been confirmed experimentally by Buttner et al.[8]. The ordering strongly reduces the overlap between adjacent Cu sites. Kugel and Khomskii appear to have been the first to demonstrate that this leads to a small ferromagnetic exchange constant in the orbitally-ordered planes [2]. The Jahn-Teller distorted Cu octahedra in this structure are similar to those in many high-Tc superconducting cuprate perovskites, and thus KCuF3 models certain aspects of these materials. On this basis, Buttner et al. have suggested a vibrationally-modulated exchange mechanism for superconductivity [8, 9].
The only previous ab initio theoretical calculation for similar perovskites of which we are aware is the recent study of Eyert and Hock [6], who examined K2NiF4 and K2CuF4 within the local spin density approximation (LSDA). This latter material shows similar antiferrodistortive behaviour to KCuF3 but contains well-separated two-dimensional CuF2 planes, rather than CuF6 octahedra. These authors came to the conclusion that ‘both magnetism and orthorhombic distortion [are] required in order to arrive at the insulating ground state’ which they define as the presence of zero density of states at the Fermi energy; their calculations did not lead to the presence of an actual gap in the band structure. This unphysical feature of their calculations presumably results from the local approximation to the non-local exchange operator implicit in the LSDA [10] with consequent large self-interaction errors. The correct treatment of the non-local part of the Hamiltonian is crucial in determining the orbital dependence of the one-electron potential and thus the ordering of the d states in the eigenvalue spectrum. Orbital ordering of the K2CuF4 electron density was not reported in this study.
All calculations reported in the present work were performed using a pre-release of the program CRYSTAL95 [36], a development of the well-established CRYSTAL92 package [12]. This code may be used to perform open-shell calculations within the unrestricted Hartree-Fock approximation. The solid-state band structure problem is solved in a basis of Bloch functions constructed from linear combinations of localized atomic orbitals, which are in turn a sum of Gaussian-type primitives. Reference may be made to a previous study of KNiF3 [1] for computational details of the present calculations, including exponents and contraction coefficients of the K and F bases, and to references [11-13] for a discussion of the theoretical method. Other applications of this method to compounds containing transition metals include MnO and NiO [3-5], Fe2O3 [14], FeF2 [37], MgO-NiO thin films [15], Li-doped NiO and MnO [16] and the perovskites KNiF3 [1] and K2NiF4 [17]. Some interesting questions relevant to the present work were addressed in the latter two studies, and will be referred to in context in the discussion that follows.
The principal source of error in the Hartree-Fock approach is the neglect of electron Coulomb correlation. In ‘'strongly-correlated' materials’ such as KCuF3 this manifests itself as a short-range screening effect which is much less crucial to the qualitative features of the ground state of magnetic insulators than the non-local exchange. Our code permits correlation corrections to be applied to the Hartree-Fock energy at varying levels of sophistication [18, 19]. The most approximate method involves a posteriori correlation corrections to the total energy using various functionals of the electron density. In this paper, we examine the effect of applying such a functional on a number of ground state properties calculated from the total energy. A more sophisticated approach that has been incorporated into the code involve the use of correlation-only functionals within a Kohn-Sham-like Hamiltonian. The effect of this combination of density-functional correlation and exact Hartree-Fock non-local exchange on results for magnetic insulators is under investigation and will be reported subsequently.
Results and Discussion
Geometry
First of all, some simple calculated structural properties are compared
with experimental data. In Table 1, the equilibrium
values of a, c and the fluorine coordinate xF
are shown. These were calculated for the untwisted structural polytype
of KCuF3 in the AF1 spin state. The values
of a and c are 2.4% and 3.8% greater than experiment. While
the error in a is roughly equivalent to that found in previous studies
of transition-metal compounds such as MnO and NiO using this method [1,
5], the error in c is somewhat greater. This discrepancy
is however in line with results for the series Li2O,
Na2O, K2O
[20] and LiF, NaF, KF [21], which
indicate that the Hartree-Fock method routinely overestimates the size
of large cations such as K+ (the ion separating
the ab planes in KCuF3). In a subsequent
section, we will examine the behaviour of various structural and magnetic
properties as a function of a, c and xF.
Calculations of properties such as exchange constants will be performed
at the experimental geometry however, since it has been shown in
previous work [1, 17] that, in line with suggestions
made in the literature [22], the magnitude of the
exchange interaction in fully ionic compounds generally follows a d
-x power law, where d is the
interionic distance and x is between 11 and 15.
|
calc. |
expt. |
|
|
a |
5.99 |
5.85 |
|
C |
4.07 |
3.93 |
|
xF |
0.237† |
0.228 |
|
0.233‡ |
||
Table 1 - Calculated and experimental lattice parameters a and c (Å) and fluorine coordinate xF for untwisted polytype of KCuF3 with the experimental AF1 spin structure. † refers to pure Hartree-Fock calculation, ‡ to Hartree-Fock corrected a posteriori using a Perdew gradient-corrected correlation functional [24].
The calculated Hartree-Fock adiabatic potential energy surface for movement
of the F2 fluorine along the line separating nearest-neighbour Cu ions
is the upper curve shown in Fig. 2. The Cu-Cu midpoint
position is seen to be unstable, and thus this displacement co-ordinate
corresponds to a Jahn-Teller distortion of the CuF6
octahedra, with a classical double well containing two equivalent minima
[23]. The equilibrium fluorine position (Table
1) corresponding to the bottom of the well is reasonably close to the
experimental value (an error of +3.4 % of the nearest-neighbour Cu-F distance).
The lower curve in Fig. 2 shows the effect on the
shape of the double well of a posteriori gradient-corrected correlation
corrections using the Perdew functional [24]. The
two curves have been shifted to coincide at the undistorted configuration.
Compared to the straight Hartree-Fock calculation the depth of the Jahn-Teller
well is increased by around 50% (from 0.0044 to 0.0065 Hartree) and the
error in the equilibrium fluorine coordinate is roughly halved in the correlation-corrected
calculations. The energy scale associated with the co-operative Jahn-Teller
effect in KCuF3 is around 20-25 times greater
than the calculated magnetic ordering energies reported later in this section.
We have also carried out local spin density functional calculations using the same basis sets and computer code. As expected, these do not show the double well feature and the undistorted structure is predicted to be the most stable. LSDA calculations do not therefore predict the experimentally observed co-operative Jahn-Teller distortions in this material.
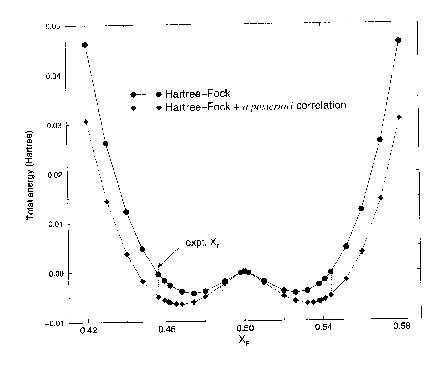
Figure 2 - Total energy (relative to the undistorted crystal) as a function of fluorine coordinate XF in the ab plane. XF = 2xF, where xF is the fractional F2 coordinate.
Finally, the total energy cost of introducing fluorine stacking disorder was estimated. The energy differences between twisted and untwisted polytypes of KCuF3 with equivalent magnetic structure and lattice parameters was found to be extremely small (an order of magnitude lower than the energy scale associated with the magnetic ordering). This is consistent with the experimental difficulty of preparing single-phase crystals. The twisted polytype, which is the predominant phase in real crystals, was the more stable of the two by around 3x10 -5 Hartree.
Orbital ordering and electronic structure
Table 2 shows the results of a Mulliken analysis of the unrestricted Hartree-Fock wave function. KCuF3 is seen to be highly ionic, with net atomic charges close to their formal values and a single d orbital hole associated with each Cu ion. Orbital populations and the coefficients of the Fock eigenvectors indicate that the hole orbital is largely constructed from a linear combination of the (non-degenerate) dz2 and dx2-y2 Bloch basis functions. The single unpaired spin associated with each hole is almost exclusively contained in the d orbitals, and there is a small amount of spin dispersion onto the fluorine ions (which is crucial for the mechanism of superexchange, as we shall see). The data are quoted for the AF1 antiferromagnetic state only, since differences in orbital populations for alternative magnetic states were found to be negligible (less than 0.002|e|).
|
AF1 |
||||
|
K |
Cu |
F1 |
F2 |
|
|
Q |
+1.00 |
+1.83 |
-0.95 |
-0.95 |
|
q (3d) |
- |
9.09 |
- |
- |
|
|
0.00 |
0.95 |
0.01 |
0.01 |
|
|
- |
0.95 |
- |
- |
Table
2 - Mulliken charges and population data
(in electrons) for AF1 antiferromagnetic KCuF3.
Q is the net atomic charge; q(3d) is the electron
population of the d orbitals; ![]() and
and ![]() are the magnitudes
of the corresponding spin quantities.
are the magnitudes
of the corresponding spin quantities.
The total charge density in the Jahn-Teller distorted ab plane
is shown on a relatively small scale in Fig. 3(a).
A close-up of a single ‘cell’ in this plane in Fig.
3(b) shows the difference between the total charge density and a superposition
of spherical ionic densities. Such plots indicate the changes in shape
of the spherically symmetric free-ion electron distributions due to the
influence of the crystalline environment. The effect of orbital ordering
on the density difference map in Fig. 3(b) is particularly
striking; the copper hole orbital alternates between the ‘dx2-z2’
and ‘dy2-z2’ orbitals on adjacent Cu ions. Fig.
3(c) show the equivalent plot for the plane perpendicular to ab
containing the undisplaced F1 ions. In this case, no ordering of the electron
density is associated with F1 and the Cu-F-Cu vector is a standard 180
degree superexchange contact which would be expected to give rise to an
antiferromagnetic spin ordering of the two coppers along the c axis.
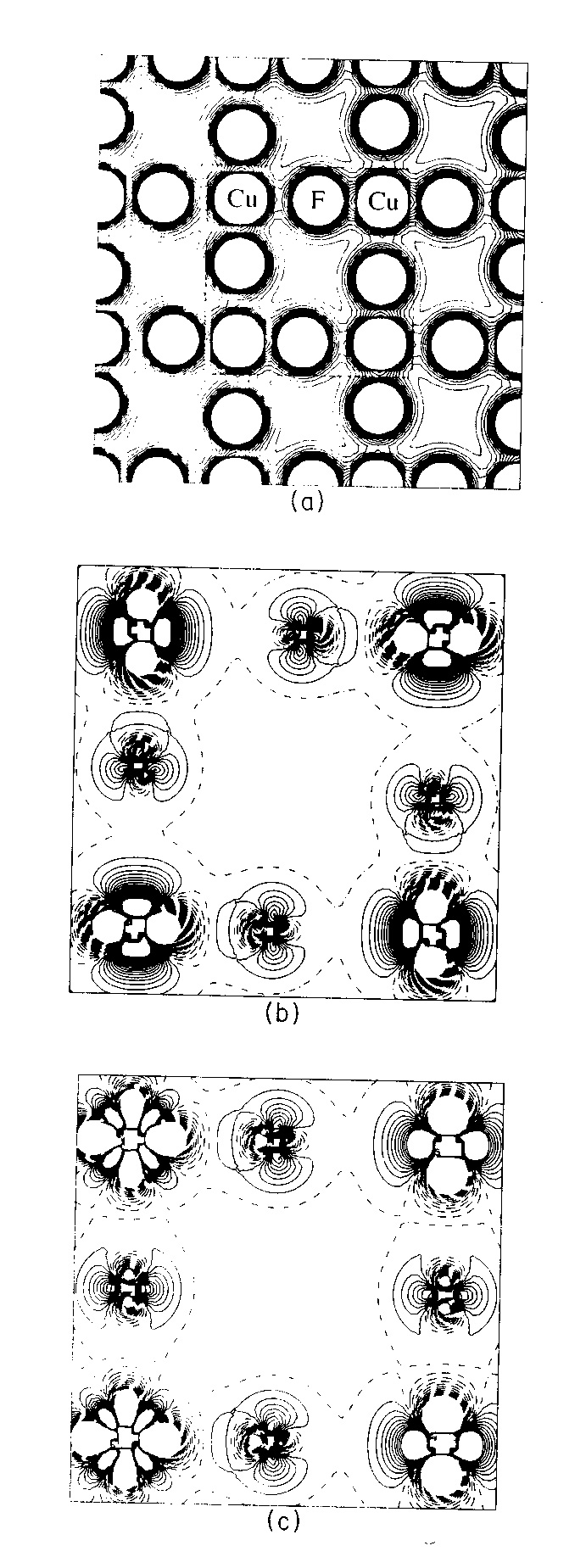
Figure 3 - (a) Total charge density map in the ab (001) plane of KCuF3 through the Cu and F ions. The separation between adjacent isodensity curves is 0.01 e/bohr3; the innermost curves in the atomic region correspond to 0.15 e/bohr3. The dashed box denotes the area of Fig. (b) which is a charge density difference map in the ab plane for AF1 KCuF3. Fig. (c) is the equivalent plot in the ac plane. Both (b) and (c) refer to the difference between the bulk density and the density obtained as a superposition of spherical ionic densities (using the same basis set in both cases). Continuous, dashed and dot-dashed lines correspond to positive, negative and zero values respectively. The separation between adjacent isodensity curves is 0.005 e/bohr3; the innermost curves in the atomic region correspond to 0.05 e/bohr3.
To understand the Hartree-Fock electronic structure, it is useful to examine the calculated density of states (DOS). The standard definition of the tetragonal cell is such that it was necessary to rotate the Cartesian reference frame around the z axis by 45 degrees, in order to align the lobes of the dx2-y2 functions along the Cu-F-Cu vectors. Band-projected DOS using the conventional atomic orbital symmetries could then be calculated. This unitary transformation does not of course affect the ground-state properties, but mixes the orbitals among themselves changing the orbital populations and the projected DOS. The valence band of the latter is plotted in Fig. 4. KCuF3 is correctly predicted to be a wide band gap insulator, with states at the top of the valence band of predominantly fluorine 2p character, and metal 3d states at the bottom of the conduction band. It is thus a charge-transfer insulator in the Zaanen-Sawatzky-Allen classification scheme [25]. The effect of the magnetic order on the density of states was found to be comparatively small. The magnitude of the band gap (which is overestimated in the Hartree-Fock scheme) was 0.65 Hartree.
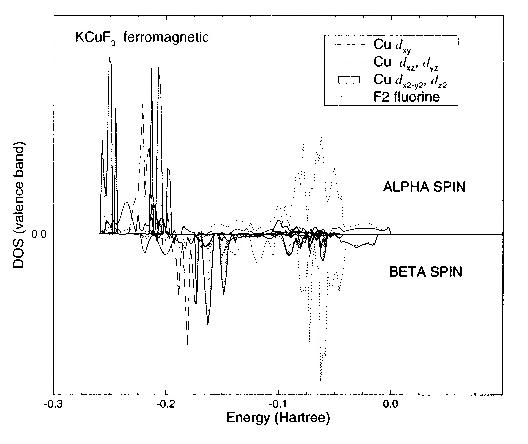
Figure 4 - Valence band projected density of states for ferromagnetic phase of KCuF3. Energy relative to the highest occupied level.
Magnetic properties
As discussed by P.W. Anderson in his original work on superexchange [26], all the elements necessary to describe this interaction are present in principle in the unrestricted Hartree-Fock theory. In this section therefore, we shall attempt to calculate exchange constants, and describe how the sign of the interaction may change depending on the degree of spin-orbital overlap, mediated by orbital ordering effects.
The calculations correctly predict the antiferromagnetic (AF1) spin
state to be the most stable magnetic phase, followed by the ferromagnetic
which is in turn very slightly more stable than the AF2. The differences
in total energy per Cu ion between these states (![]() )
may be approximately related to data derived from various kinds of experiment
[27-30]. Such data are normally interpreted in terms
of the magnetic coupling constants J of a model spin Hamiltonian,
such as the Ising or Heisenberg models. As the solutions of the unrestricted
Hartree-Fock equations are eigenfunctions of the
)
may be approximately related to data derived from various kinds of experiment
[27-30]. Such data are normally interpreted in terms
of the magnetic coupling constants J of a model spin Hamiltonian,
such as the Ising or Heisenberg models. As the solutions of the unrestricted
Hartree-Fock equations are eigenfunctions of the ![]() z
spin operator but not of the total spin operator
z
spin operator but not of the total spin operator ![]() ,
the former model is more appropriate in this case. Within the Ising model
therefore, and assuming coupling only between nearest Cu neighbours, the
following expression relates J to
,
the former model is more appropriate in this case. Within the Ising model
therefore, and assuming coupling only between nearest Cu neighbours, the
following expression relates J to ![]() ,
,
![]()
Here S is the total spin per Cu ion (assuming for the moment the calculated value of 0.476 from a Mulliken analysis) and z is the number of nearest neighbours of a given Cu that have differing spins in the two magnetic states. The appearance of the factor z in this equation is dependent upon the assumption that the exchange interactions are additive, that is, directly proportional to the number of nearest neighbours of a given Cu. Previous studies of KNiF3 and K2NiF4 are consistent with this assumption, since, for example, the ratio of the calculated E values was very close to the 6:4 ratio of the number of Ni neighbours [1, 17].
In Table 3, exchange constants estimated within
the Ising model from the Hartree-Fock data are compared with the corresponding
experimental values (as is customary, the exchange constants in energy
units are divided by Boltzmann's constant to yield quantities with the
dimensions of temperature). The qualitative features of the calculated
exchange constants (model 1) are essentially correct; Jc
is negative in sign (antiferromagnetic) and very much larger than Ja,
which is small and positive (ferromagnetic). Hence the one-dimensional
nature of the magnetic interactions in KCuF3
is reproduced. The quantitative agreement in Jc
is rather poor however, and there are likely to be a number of reasons
for this. One of the principal problems appears to be the experimentally
well-characterized zero-point deviations in the spin direction, which are
included neither in the Hartree-Fock theory nor in the Ising model we use
to interpret the data in terms of exchange constants. Such effects are
particularly important in low-dimensional magnetic systems such as KCuF3,
and have two principal consequences [27]. The first
of these is a lowering of the expected on-site magnetic moment of ![]() to
to ![]() , where
, where ![]() is the anisotropy-dependent spin reduction. The second effect is an enhanced
stabilization of the antiferromagnetic state relative to the ferromagnetic.
An interesting strategy is to consider the fully-aligned Néel antiferromagnetic
state assumed implicitly in our Hartree-Fock treatment as an approximate
ground state, and to correct for zero-point effects using corrections to
the basic Ising model. The simplest modification consists of replacing
S in Eq. (1) by
is the anisotropy-dependent spin reduction. The second effect is an enhanced
stabilization of the antiferromagnetic state relative to the ferromagnetic.
An interesting strategy is to consider the fully-aligned Néel antiferromagnetic
state assumed implicitly in our Hartree-Fock treatment as an approximate
ground state, and to correct for zero-point effects using corrections to
the basic Ising model. The simplest modification consists of replacing
S in Eq. (1) by ![]() ,
where
,
where ![]() is calculated
from the difference between the calculated Hartree-Fock magnetic moment
(0.95
is calculated
from the difference between the calculated Hartree-Fock magnetic moment
(0.95![]() ) and the spin-reduced
experimental value (0.48
) and the spin-reduced
experimental value (0.48![]() measured
at 4 K) [7]. The resulting exchange constants are
shown in Table 3 (Model 2). The quantitative agreement
between theory and experiment after making this correction is good. To
take into account the enhanced stabilization of the antiferromagnetic state,
a model correction must be applied to the calculated value of
measured
at 4 K) [7]. The resulting exchange constants are
shown in Table 3 (Model 2). The quantitative agreement
between theory and experiment after making this correction is good. To
take into account the enhanced stabilization of the antiferromagnetic state,
a model correction must be applied to the calculated value of ![]() .
The relevant formula is discussed by de Jongh et al. [27],
and takes the following form:
.
The relevant formula is discussed by de Jongh et al. [27],
and takes the following form:
![]()
Here ![]() is the magnetic anisotropy
and
is the magnetic anisotropy
and ![]() is a function which
varies from
is a function which
varies from ![]() to
zero for
to
zero for ![]() . Intermediate
values of this function can be calculated from spin-wave theory. Assumption
of
. Intermediate
values of this function can be calculated from spin-wave theory. Assumption
of ![]() and the spin-reduced
value of S and hence the maximum correction for KCuF3
gives Ja = +5 and Jc
= -229 K; both exchange constants are thus corrected in the right direction.
and the spin-reduced
value of S and hence the maximum correction for KCuF3
gives Ja = +5 and Jc
= -229 K; both exchange constants are thus corrected in the right direction.
|
Exchange constants (K) |
|||
|
experimental |
Model 1 |
Model 2 |
|
|
Ja |
+2 [d] |
+1 |
+6 |
|
Jc |
-187[a], -190[b], -197 [c], -203 [d] |
-46 |
-182 |
Table 3 - Calculated and experimental exchange constants in KCuF3. The experimental results were derived from [a] = - magnetic specific heat [32], [b] - susceptibility [33], [c] - neutron diffraction [34], [d] - neutron diffraction [35]data. Model 1 = Eq. (1). with calculated S (=0.476), model 2 = Eq. (1) with experimental S (=0.24).
Apart from zero-point effects, other factors that could influence the
comparison of our calculations with experiment are spin-orbit coupling,
spin contamination and the neglect of electron correlation. For systems
with partly filled shells of ‘eg’
orbitals, such as the Cu2+ ion, the orbital
angular momentum is completely quenched [31], and
so the effect of spin orbit-coupling terms should be inconsequential. Spin
contamination is associated with the fact that the unrestricted Hartree-Fock
wave function is not an eigenfunction of the ![]() operator,
and involves the admixture of high energy components with differing spin
multiplicities into the wave function. We are not able to quantify the
magnitude of this effect at present.
operator,
and involves the admixture of high energy components with differing spin
multiplicities into the wave function. We are not able to quantify the
magnitude of this effect at present.
We may estimate the effect of electron correlation on the calculated
values of ![]() in a
rather approximate way through a posteriori evaluation of an appropriate
density functional of the converged Hartree-Fock density. We have used
the gradient-corrected correlation functional proposed by Perdew et
al. [24]. For KCuF3,
the correlation energy in the ferro- and antiferromagnetic states was found
to be the same to within 10-4 Hartree (the range within which
the necessary numerical integration of the electron density may be considered
reliable). Within the approximation of this functional, this implies a
maximum correlation contribution to
in a
rather approximate way through a posteriori evaluation of an appropriate
density functional of the converged Hartree-Fock density. We have used
the gradient-corrected correlation functional proposed by Perdew et
al. [24]. For KCuF3,
the correlation energy in the ferro- and antiferromagnetic states was found
to be the same to within 10-4 Hartree (the range within which
the necessary numerical integration of the electron density may be considered
reliable). Within the approximation of this functional, this implies a
maximum correlation contribution to ![]() in KCuF3 of around 5x10-5 Hartree,
or 18%. Other workers have examined magnetic interactions in KNiF3
using a cluster model [39] and suggest that the correlation
energy evaluated with second-order perturbation theory contributes up to
50% to
in KCuF3 of around 5x10-5 Hartree,
or 18%. Other workers have examined magnetic interactions in KNiF3
using a cluster model [39] and suggest that the correlation
energy evaluated with second-order perturbation theory contributes up to
50% to ![]() . This may be compared
with our calculated value for the same system of around 25%. While the
use of the cluster approach in modelling infinite systems requires some
caution, the effect of electron correlation on the relative energies of
different magnetic states remains a delicate open question.
. This may be compared
with our calculated value for the same system of around 25%. While the
use of the cluster approach in modelling infinite systems requires some
caution, the effect of electron correlation on the relative energies of
different magnetic states remains a delicate open question.
We shall now examine the mechanism of the exchange interactions in KCuF3.
The reason why the exchange constant |Ja|
is very small and ferromagnetic in the orbitally-ordered plane is related
to the degree of overlap of the Fock spin orbitals along the a and
c axes. This may be appreciated from Fig. 5,
in which the variation of the calculated ![]() with fluorine coordinate is shown. With the F2 fluorine in the undistorted
position (very weak orbital ordering) the exchange is strongly antiferromagnetic,
while as the octahedra are progressively distorted, it first becomes weakly
ferromagnetic and then antiferromagnetic again at even higher distortions.
The almost vanishing value of |Ja|
observed experimentally might thus be said to be an essentially ‘accidental’
structural feature; the range of the fluorine co-ordinate over which
with fluorine coordinate is shown. With the F2 fluorine in the undistorted
position (very weak orbital ordering) the exchange is strongly antiferromagnetic,
while as the octahedra are progressively distorted, it first becomes weakly
ferromagnetic and then antiferromagnetic again at even higher distortions.
The almost vanishing value of |Ja|
observed experimentally might thus be said to be an essentially ‘accidental’
structural feature; the range of the fluorine co-ordinate over which ![]() is ferromagnetic is around 8% of the nearest-neighbour Cu-F distance. We
will now discuss this behaviour quantitatively through a consideration
of the kinetic, Coulomb, exchange and correlation contributions to the
total energy in the various magnetic states.
is ferromagnetic is around 8% of the nearest-neighbour Cu-F distance. We
will now discuss this behaviour quantitatively through a consideration
of the kinetic, Coulomb, exchange and correlation contributions to the
total energy in the various magnetic states.
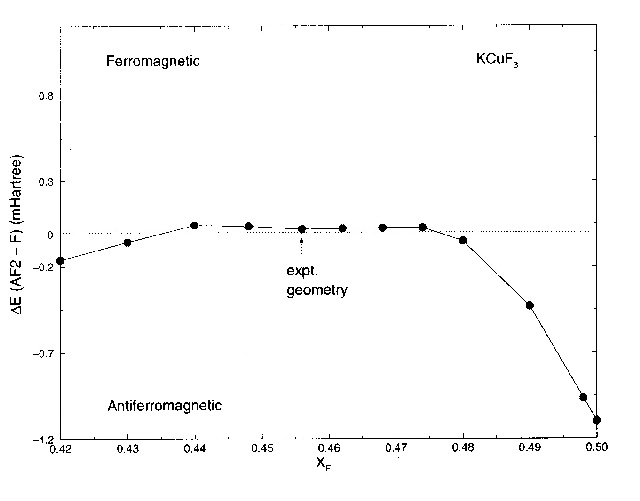
Figure 5 - Energy
difference ![]() per formula
unit between the ferromagnetic and AF2 antiferromagnetic phases as a function
of the fluorine coordinate XF
in the ab plane (XF
= 2xF).
per formula
unit between the ferromagnetic and AF2 antiferromagnetic phases as a function
of the fluorine coordinate XF
in the ab plane (XF
= 2xF).
In a standard M—F—M superexchange contact, it is well known that the predominant contribution to the additional stability of the antiferromagnetic state is the lowering of the kinetic energy in this phase [26]. In his original formulation of superexchange theory, Anderson introduced the concepts of ‘kinetic exchange’ and ‘potential exchange’ to clarify the major interaction terms [26]. In the Hartree-Fock picture, kinetic exchange is a consequence of antisymmetrization and arises in the following way. If two neighbouring spins are parallel, their spatial orbitals must be orthogonal, but when they are antiparallel, the spin functions are automatically orthogonal so the orbitals may overlap each other. This may be thought of as a ‘Pauli repulsion’ between electrons of the same spin. There is a significant kinetic energy gain when antiparallel spins are present, and hence this term is antiferromagnetic in sign. The magnitude of the kinetic exchange, which is proportional to the degree of spin orbital overlap, is normally estimated using a perturbation theoretical approximation to the Hubbard model. In the case of small overlap, the most important interaction term is the potential exchange arising from Coulomb interactions, which is always ferromagnetic in sign.
In Table 4, an analysis of the various contributions
to the total energy is given for the various magnetic states of KCuF3.
Terms in the kinetic, Coulomb and exchange energy are evaluated, together
with an a posteriori evaluation of the correlation energy using
the Perdew scheme. The Ewald convention used in performing the infinite
lattice sums does not permit a strict partitioning of the Coulomb energy
into nuclear attraction and electron repulsion terms [38].
For comparative purposes, we also show the equivalent data for four other
antiferromagnetic compounds investigated by us using the same method. In
these latter materials, the major magnetic interactions are all through
standard 180 degree superexchange contacts. For each system, the total
energy difference between ferro- and antiferromagnetic states at the same
geometry is ‘normalized’ to -1, and differences in the various components
of the total energy between the two phases defined relative to this. Apart
from the interaction in the orbitally-ordered plane of KCuF3,
the dominant contribution to the energy lowering in the antiferromagnetic
phase is in each case the kinetic energy term. The ferromagnetic superexchange
contact in KCuF3 shows quite different
characteristics however. Because of the small overlap in the orbitally-ordered
plane, the difference in kinetic energy between the AF2 and ferromagnetic
phases is relatively small, and the dominant contribution to the energy
difference is the additional electron-nuclear attraction in the ferromagnetic
phase. The contribution of the correlation energy to ![]() is not insignificant, but a quantitative analysis using density functionals
of the electron density requires higher accuracy in the numerical integration
of the electron density.
is not insignificant, but a quantitative analysis using density functionals
of the electron density requires higher accuracy in the numerical integration
of the electron density.
|
(mHartree) |
|
|
|
|
(mHartree) |
|
|
KCuF3 - AF1 |
-0.265 |
-1.0 |
-15.1 |
+9.6 |
+4.5 |
0.0 |
|
KCuF3 - AF2 |
+0.017 |
+1.0 |
-4.7 |
+8.2 |
-2.5 |
0.0 |
|
KniF3 |
-1.136 |
-1.0 |
-8.4 |
+4.4 |
+3.0 |
-0.3 |
|
K2NiF4 |
-0.793 |
-1.0 |
-18.4 |
+13.7 |
+3.7 |
-0.2 |
|
NiO |
-0.608 |
-1.0 |
-13.0 |
+8.4 |
+3.6 |
-0.1 |
|
MnO |
-0.242 |
-1.0 |
-26.3 |
+15.8 |
+9.5 |
-0.1 |
Table
4 - Analysis of the various contributions
to the energy difference ![]() between
antiferro- and ferromagnetic states of various materials, including untwisted
KCuF3.
The various
between
antiferro- and ferromagnetic states of various materials, including untwisted
KCuF3.
The various ![]() data
are given in units of the difference in Hartree-Fock total energies,
data
are given in units of the difference in Hartree-Fock total energies, ![]() .
The value of
.
The value of ![]() is the difference
in correlation energy of the two magnetic states evaluated a posteriori
using the density functional of Perdew et al. [24]. Only one decimal
figure is given for this quantity, due to limitations in accuracy of the
numerical integration of the energy functional. All energy data in both
ferro- and antiferromagnetic states are evaluated at the same (experimental)
crystal geometry.
is the difference
in correlation energy of the two magnetic states evaluated a posteriori
using the density functional of Perdew et al. [24]. Only one decimal
figure is given for this quantity, due to limitations in accuracy of the
numerical integration of the energy functional. All energy data in both
ferro- and antiferromagnetic states are evaluated at the same (experimental)
crystal geometry.
The superexchange mechanism can be appreciated in a relatively simple
visual way from maps of the spin density distributions. First of all, we
consider the standard antiferromagnetic superexchange contact along the
c-axis; spin density maps in the ac plane are shown in Fig.
6(a-b). In the ferromagnetic state, the contraction of majority (alpha)
spin density on the F1 fluorine ion (centre left and centre right of the
figure) is very large relative to that of the beta spin density. This is
because of the large Pauli repulsion from unpaired alpha density on each
of two neighbouring Cu atoms. In the antiferromagnetic states, there is
a spin polarization of the fluorine ion, since the spatial orbitals
are no longer constrained to be orthogonal, and thus the exchange repulsion
may be reduced by shifting alpha density towards the Cu ion with beta polarization,
and vice versa. The closer average confinement of electrons on the fluorine
site in the ferromagnetic state ensures the dominant contribution to the
total energy is the kinetic energy term. Figs. 6(c-d)
show total spin-density maps in the ab plane for the ferromagnetic
and AF2 phases of KCuF3. Since the spin-orbital
overlap is small, no large-scale changes in spin density between the magnetic
phases are observed, and the sign and magnitude of the energy difference
between the two results from a delicate balance of the kinetic and potential
components of the total energy.

Figure 6 - Spin density maps for (a) ferromagnetic and (b) AF1 antiferromagnetic solutions in the ac plane, and (c) ferromagnetic and (d) AF2 antiferromagnetic solutions in the ab plane. Scale and symbols as in Fig. 3(b).
Finally, the variation of ![]() ,
and hence the calculated exchange constants, is examined as a function
of relatively large geometrical distortions. Fig 7(a)
shows
,
and hence the calculated exchange constants, is examined as a function
of relatively large geometrical distortions. Fig 7(a)
shows ![]() as a function
of a, and Fig. 7(b) shows
as a function
of a, and Fig. 7(b) shows ![]() versus c. In each case
versus c. In each case ![]() changes markedly as the lattice parameter is varied over
changes markedly as the lattice parameter is varied over ![]() ,
and thus the use of the experimental crystal geometry in carrying out the
exchange constant analysis is important.
,
and thus the use of the experimental crystal geometry in carrying out the
exchange constant analysis is important.
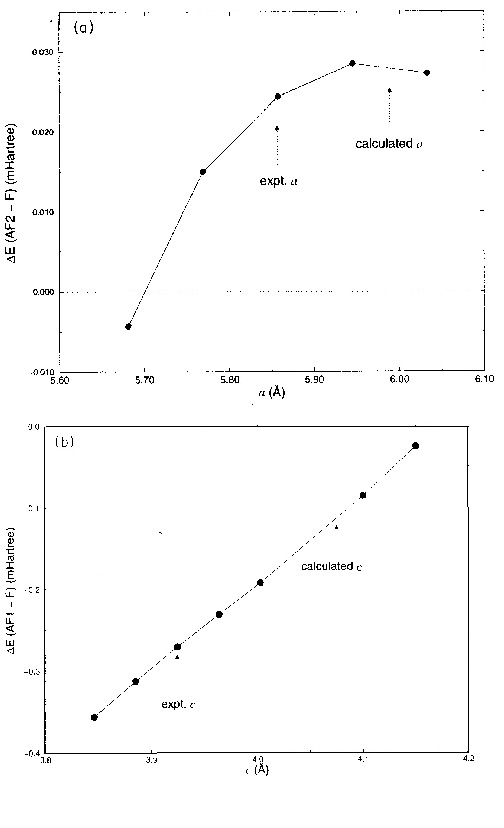
Figure 7 - Energy
difference ![]() per formula
unit between (a) ferromagnetic and AF2 antiferromagnetic phases as a function
of the a parameter, and (b) ferromagnetic and AF1 antiferromagnetic phases
as a function of the c parameter. In (a), the fluorine coordinate in the
ab plane was the calculated equilibrium value for each geometry: the equilibrium
value of XF varied between 0.469 and 0.474 as a was changed by
per formula
unit between (a) ferromagnetic and AF2 antiferromagnetic phases as a function
of the a parameter, and (b) ferromagnetic and AF1 antiferromagnetic phases
as a function of the c parameter. In (a), the fluorine coordinate in the
ab plane was the calculated equilibrium value for each geometry: the equilibrium
value of XF varied between 0.469 and 0.474 as a was changed by ![]() .
.
Conclusion
The ab initio periodic unrestricted Hartree-Fock method has been used to examine the ground-state electronic and magnetic properties of KCuF3. The material is correctly predicted to be an orbitally-ordered wide band gap insulator. The Jahn-Teller distortion of the CuF6 octahedra is reproduced, with the equilibrium distortion close to that observed experimentally. The qualitative one-dimensional features of the magnetic interactions emerge naturally from the calculation, but for a low-dimensional system such as KCuF3, the importance of higher order terms in the spin is such that interpretation of the Hartree-Fock data through an Ising type model is not appropriate. By treating the magnetic moment as a parameter, and using the experimental value to take into account the observed spin reduction, we were able to get quantitative agreement of the experimental exchange constants with the ab initio Hartree-Fock data. The influence of co-operative Jahn-Teller distortions on the exchange interaction was also analyzed, via an analysis of the various contributions to the total energy. For antiferromagnetic superexchange contacts, the lowering of kinetic energy is the dominant contribution, while in the equivalent ferromagnetic interaction in orbitally-ordered planes, the electron-nuclear repulsion predominates.
Acknowledgements
MDT wishes to thank the Commission of the European Communities for the award of a fellowship under the Human Capital and Mobility Programme (contract no. ERBCHBICT941605). The work was also partially supported by EC HC&M contract no. CHRX-CT93-0155.
References
1. J.M. Ricart, R. Dovesi, V.R. Saunders and C. Roetti, Phys. Rev. B, in press (1995).
2. D.I. Khomskii and K.I. Kugel, Solid State Commun. 18, 433 (1976) ; see K.I. Kugel and D.I. Khomskii, Sov. Phys. Usp 25, 231 (1982) for a more recent review of the subject.
3. W.C. Mackrodt, N.M. Harrison, V.R. Saunders, N.L. Allan, M.D. Towler, E. Aprà and R. Dovesi, Phil. Mag. A 68, 653 (1993).
4. M.D. Towler, Ph.D. Thesis, University of Bristol, U.K. (1994).
5. M.D. Towler, N.L. Allan, N.M. Harrison, V.R. Saunders, W.C. Mackrodt, E. Aprà, Phys. Rev. B 50, 5041 (1994).
6. V. Eyert and K.H. Hock, J. Phys.: Cond. Matter 5, 2987 (1993).
7. M.T. Hutchings, E.J. Samuelson, G. Shirane and K. Hirakawa, Phys. Rev. 188, 919 (1969).
8. R.H. Buthner, E.N. Maslen and N. Spadaccini, Acta. Crys. B 46, 131 (1990).
9. R.H. Buthner, E.N. Maslen and N. Spadaccini, Acta. Crys. B 48, 21 (1992).
10. B. Brandow, J. Alloys and Compounds 181, 377 (1992).
11. C. Pisani, R. Dovesi and C. Roetti, Hartree-Fock ab initio treatment of crystalline systems, Lecture Notes in Chemistry 48 (Springer, Berlin, 1988).
12. R. Dovesi, V.R. Saunders and C. Roetti, CRYSTAL 92 user documentation (Università di Torino, Torino, 1992).
13. E. Aprà, Ph.D. Thesis, Università di Torino, Italy (1993).
14. M. Catti, G. Valerio and R. Dovesi, Phys. Rev. B., accepted (1994).
15. M.D. Towler, N.M. Harrison and M.I. McCarthy, Phys. Rev. B, 52, 5375 (1995).
16. W.C. Mackrodt, N.M. Harrison, V.R. Saunders, N.L. Allan and M.D. Towler, Chem. Phys. Lett. 250, 66 (1996).
17. R. Dovesi, J.M. Ricart, V.R. Saunders and R. Orlando, submitted to J. Phys. C.
18. M. Causà and A. Zupan, Chem. Phys. Lett. 220, 145 (1994).
19. M. Causà and A. Zupan, Int. J. Quant. Chem., S28, 633 (1995).
20. R. Dovesi, C. Roetti, C. Freyria-Fava, M. Prencipe and V.R. Saunders, Chem. Phys. 156, 11 (1991).
21. M. Prencipe, A. Zupan, E. Aprà, R. Dovesi and V.R. Saunders, Phys. Rev. B 51, 3391 (1995).
22. L.J. de Jongh and R. Block, Physica B 79, 568 (1975).
23. M.C.M. O’Brien and C.C. Chancey, Am. J. Phys. 61, 688 (1993).
24. J.P. Perdew, J.A. Chevary, S.H. Vosko, K.A. Jackson, M.R. Pederson, D.J. Singh and C. Fiolhais, Phys. Rev. B 46, 6671 (1992).
25. J. Zaanen, G.A. Sawatzky and J.W. Allen, Phys. Rev. Lett. 55, 418 (1995).
26. P.W. Anderson, Solid State Phys. 14, 99 (1963).
27. L.J. de Jongh and A.R. Miedema, Adv. Phys. 23, 1 (1974), see p. 181
28. L.J. de Jongh, AIP Conf. Proceed. 10, 561 (1973).
29. H.W. de Wijn, L.R. Walker and R.F. Walstedt, Phys. Rev. B 8, 285 (1973).
30. J. Skalyo Jr., G. Shirane, R.J. Birgeneau and H,J, Guggenheim, Phys. Rev. Lett 23, 1394 (1969).
31. see, for example, A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions (Clarendon Press, Oxford, 1970).
32. K. Iio, H. Hyodo, K. Nagata and I. Yamada, J. Phys. Soc. Jpn. 44, 1393 (1978).
33. S. Kadota, I. Yamada, S. Yoneyama and K. Hirakawa, J. Phys. Soc. Jpn. 23, 751 (1967).
34. M.T. Hutchings, H. Ikeda and J.M. Milne, J. Phys. C 12, L739 (1979).
35. K. Satija, J.D. Axe, G. Shirane, H. Yoshizawa and K. Hirakawa, Phys. Rev. B 21, 2001 (1980).
36. CRYSTAL 95, University of Torino and DRAL Daresbury Laboratory.
37. G. Valerio, M. CAtti, R. Dovesi and R. Orlando, Phys. Rev. B, in press (1995).
38. V.R. Saunders, C. Freyria-Fava, R. Dovesi, L. Salasco and C. Roetti, Mol. Phys. 77, 629 (1992).
39. J.A. Mejías and J.F. Sanz, J. Chem. Phys. 102, 850 (1995)