![]() .
.
Density functional theory in periodic systems using local Gaussian basis sets
Michael D. Towler and Mauro Causà
Gruppo di Chimica Teorica, Dipartimento CIFM, Universita di Torino, I-10100 Torino, Italy
Ales Zupan,
Department of Environmental Sciences, Jozef Stefan Institute, Jamova 39, 61111 Ljubljana, Slovenia
{appeared in Computer Physics Communications 98, pp. 181-205 (1996)}
Abstract
This paper describes a new implementation of density functional theory for periodic systems in a basis of local Gaussian functions, including a thorough discussion of the various algorithms. The results of test calculations using this scheme are reported for some representative crystalline solids, with particular emphasis placed on the influence of the various computational parameters used to control the accuracy of the numerical integration of the exchange-correlation potential.
Introduction
The computer code CRYSTAL [1] is an implementation of the Hartree-Fock (HF) method for periodic systems, and has now been under continuous development for over twenty years. It is a reliable tool for computing the electronic structure and associated ground-state properties of up to three-dimensionally periodic materials within the Hartree-Fock approximation. The Bloch functions of a periodic system are expanded as linear combinations of atom-centred Gaussian functions, and the use of efficient integral evaluation algorithms and powerful screening techniques which exploit the real space locality combine to produce a code which is both fast, and scales attractively (linearly for the integrals calculation in many cases) with the number of basis functions. The latest version of this code [2] includes a number of major innovations, one of the most important of which is the additional capability of calculating the electronic structure of materials within density functional theory (DFT) or various hybrid approximations containing elements of both Hartree-Fock and Kohn-Sham Hamiltonians. Thus the new code may be used to perform consistent comparisons between the Hartree-Fock and Kohn-Sham descriptions of the structural, electronic and magnetic properties of molecules, polymers, surfaces and crystalline solids using identical basis sets and computational conditions.
In the following presentation, the computational implementation of the density functional theory within CRYSTAL will first be outlined, emphasizing the necessary modifications to the algorithms of the original code. In particular, the techniques used to carry out the numerical integrations required in the solution of the Kohn-Sham equations are discussed in detail. Properties of the various local and gradient-corrected exchange-correlation functionals and potentials included in the code are given in an appendix. Finally, results are presented to demonstrate the dependence of various calculated observables on the computational parameters used to control the accuracy of the calculation. Specifically, the dependence of the calculated equilibrium geometries, bulk moduli, atomization energies and band structures of Si, NaCl and Al on the accuracy of the numerical integration of the total energy and Kohn-Sham matrix elements, and on the auxiliary basis set used to expand the exchange-correlation potential are reported. These results are used to define default values for the computational parameters.
Theoretical and computational method
Basic equations
The crystalline-orbital method upon which our treatment is based is an extension of standard LCAO molecular-orbital techniques to periodic systems, where the wave function must obey the Bloch theorem,
![]() .
.
The wave vector k is the generating vector of the irreducible
representation of the group of crystal translations {g}. The electron
density ![]() of an N-electron
system described by such a wave function is given from the optimum one-electron
crystalline orbitals
of an N-electron
system described by such a wave function is given from the optimum one-electron
crystalline orbitals ![]() by
by
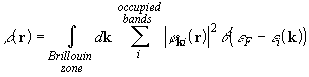 ,
,
where (theta) is the Heaviside step function, ![]() is the k-dependent eigenvalue of the ith crystalline orbital,
and the Fermi energy
is the k-dependent eigenvalue of the ith crystalline orbital,
and the Fermi energy ![]() determines
the occupied manifold in k-space. The unknown crystalline orbitals
are expanded as linear combinations of a set of m Bloch functions
built from local atom-centred Gaussian-type functions
determines
the occupied manifold in k-space. The unknown crystalline orbitals
are expanded as linear combinations of a set of m Bloch functions
built from local atom-centred Gaussian-type functions ![]() ,
,
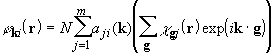 ,
,
and are solutions of the one-particle equations
![]() .
.
The principal difference between the Kohn-Sham density functional
and Hartree-Fock methods lies in the form of the one-electron operator
![]() . The Hartree-Fock monoelectronic
operator is given by
. The Hartree-Fock monoelectronic
operator is given by
![]() ,
,
where ![]() ,
, ![]() ,
,
![]() , and
, and ![]() are respectively the kinetic, external potential, Coulomb and non-local
exchange operators. The Kohn-Sham monoelectronic operator is defined as
are respectively the kinetic, external potential, Coulomb and non-local
exchange operators. The Kohn-Sham monoelectronic operator is defined as
![]() ,
,
where ![]() is the exchange-correlation
potential operator, that is, the functional derivative of the exchange-correlation
density functional energy
is the exchange-correlation
potential operator, that is, the functional derivative of the exchange-correlation
density functional energy ![]() with
respect to the density at a point r,
with
respect to the density at a point r,
![]() .
.
In a local density approximation (LDA), ![]() is defined in terms of the exchange-correlation energy per particle
is defined in terms of the exchange-correlation energy per particle ![]() in a uniform electron gas of density
in a uniform electron gas of density ![]() ,
,
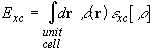 .
.
Thus modification of the existing Hartree-Fock code to perform
DFT calculations is straightforward in principle. It is required only to
delete the HF exchange ![]() and
instead to evaluate matrix elements of the
and
instead to evaluate matrix elements of the ![]() operator, that is, to evaluate the Kohn-Sham rather than the Hartree-Fock
equations at each iteration of the self-consistent field (SCF) procedure.
All other contributions to the one-electron operator are the same in both
schemes.
operator, that is, to evaluate the Kohn-Sham rather than the Hartree-Fock
equations at each iteration of the self-consistent field (SCF) procedure.
All other contributions to the one-electron operator are the same in both
schemes.
The matrix elements of the ![]() operator in a basis of Gaussian-type functions
operator in a basis of Gaussian-type functions ![]() ,
where g labels the cell containing the jth basis function
at atomic position
,
where g labels the cell containing the jth basis function
at atomic position ![]() , take the
form
, take the
form
![]() .
.
A great many analytic forms for the exchange-correlation potential
![]() have been suggested. To allow
comparisons between the various proposals [3], the most important of these
have been implemented in the new code; details of the available functionals
and potentials are given in Appendix
1. In general however, the
have been suggested. To allow
comparisons between the various proposals [3], the most important of these
have been implemented in the new code; details of the available functionals
and potentials are given in Appendix
1. In general however, the ![]() potentials have an exceedingly complex analytic form, even at a local level,
and so for periodic systems the matrix elements must be evaluated numerically.
Performing the numerical integration directly over each pair of real space
basis functions is expensive in crystalline calculations, and in the present
work a more efficient procedure has been adopted. In this method, the exchange-correlation
potential is expanded in an auxiliary basis set of contracted Gaussian-type
functions {G(r)},
potentials have an exceedingly complex analytic form, even at a local level,
and so for periodic systems the matrix elements must be evaluated numerically.
Performing the numerical integration directly over each pair of real space
basis functions is expensive in crystalline calculations, and in the present
work a more efficient procedure has been adopted. In this method, the exchange-correlation
potential is expanded in an auxiliary basis set of contracted Gaussian-type
functions {G(r)},
![]() .
.
This expansion allows the evaluation of the DFT potential integrals
in Eq. 9 as a linear combination of integrals ![]() over the auxiliary basis functions. These primitive integrals need only
be calculated once and stored:
over the auxiliary basis functions. These primitive integrals need only
be calculated once and stored:
![]() .
.
At each SCF iteration the auxiliary basis set is fitted to the actual analytic form of the exchange-correlation potential (Appendix 1), which changes with the evolving charge density. The best-fit coefficients ca are evaluated by solving the linear least-squares equation
![]() ,
,
where A is the overlap matrix between auxiliary basis functions,
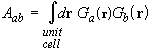 ,
,
c is the vector of unknown coefficients ca, and b is a density-dependent vector of overlap integrals between the fitting functions and the exchange-correlation potential,
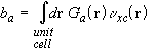 .
.
Both the ba integrals and
the elements of the A matrix are evaluated numerically to ensure
a consistent level of accuracy. The ba
integrals are much simpler than direct numerical integration of the matrix
elements ![]() , since they are restricted
to the unit cell. Furthermore, since the integrand is totally symmetric,
evaluation of the integrand may be restricted to an irreducible set of
sampling points. The algorithms adopted to carry out the numerical integrations
are discussed in detail in a later section.
, since they are restricted
to the unit cell. Furthermore, since the integrand is totally symmetric,
evaluation of the integrand may be restricted to an irreducible set of
sampling points. The algorithms adopted to carry out the numerical integrations
are discussed in detail in a later section.
The question arises of what fitting functions to use in the auxiliary
basis set for the expansion of the exchange-correlation potential. Since
![]() is a basis for the totally-symmetric
irreducible representation of the space group, the chosen auxiliary basis
functions must be totally symmetric with respect to all operations of the
space group. In this work, a universal set of atom-independent Gaussian
functions has been employed, with even-tempered exponents chosen to span
the range from 1000 down to 0.1 following earlier work by Baerends and
te Velde [4]. Functions of angular symmetry s, p, d,
f and g are available in the present implementation. For
the cubic crystals to be used as test cases in this paper only s
fitting functions are necessary, since the cubic symmetry ensures that
p, d and f functions do not contribute; tests revealed
the contribution of g functions to be negligible. Preliminary calculations
have also indicated that accurate results can be obtained using only s
functions even for non-cubic crystals, although it is desirable to use
functions of higher l to reduce the number of grid points per atom
in the numerical integration while maintaining a given level of accuracy.
An input parameter has been defined to allow a straightforward variation
in the number of fitting functions and the addition of further functions
at the bond midpoints; this will be discussed in a subsequent section.
is a basis for the totally-symmetric
irreducible representation of the space group, the chosen auxiliary basis
functions must be totally symmetric with respect to all operations of the
space group. In this work, a universal set of atom-independent Gaussian
functions has been employed, with even-tempered exponents chosen to span
the range from 1000 down to 0.1 following earlier work by Baerends and
te Velde [4]. Functions of angular symmetry s, p, d,
f and g are available in the present implementation. For
the cubic crystals to be used as test cases in this paper only s
fitting functions are necessary, since the cubic symmetry ensures that
p, d and f functions do not contribute; tests revealed
the contribution of g functions to be negligible. Preliminary calculations
have also indicated that accurate results can be obtained using only s
functions even for non-cubic crystals, although it is desirable to use
functions of higher l to reduce the number of grid points per atom
in the numerical integration while maintaining a given level of accuracy.
An input parameter has been defined to allow a straightforward variation
in the number of fitting functions and the addition of further functions
at the bond midpoints; this will be discussed in a subsequent section.
It should be noted that in many molecular LCAO codes the DFT contribution
to the effective Hamiltonian is evaluated through direct numerical integration
over all pairs of real space basis functions, a method which has also been
implemented in CRYSTAL for testing purposes. In molecular calculations
this method is comparable in cost with the fitting procedure. However,
this is not the case in solid-state work. In a periodic system the number
of significantly overlapping basis function pairs tends to be large even
with small unit cells, and the contributions of all such pairs must be
calculated for each of the grid points of the numerical quadrature. In
the fitting method by contrast, the loop over grid points is performed
only for building the vector b (Eq. 12) and the list of basis function
pairs is manipulated once. In tests during code development, the matrix
elements of the ![]() operator were
calculated for silicon using direct numerical integration. This was found
to increase the total CPU time by an order of magnitude with respect to
equivalent calculations using the fitting procedure, but the equilibrium
lattice parameter changed by less than 0.001Å and the total energy
by less than 0.1 kcal/mol.
operator were
calculated for silicon using direct numerical integration. This was found
to increase the total CPU time by an order of magnitude with respect to
equivalent calculations using the fitting procedure, but the equilibrium
lattice parameter changed by less than 0.001Å and the total energy
by less than 0.1 kcal/mol.
In addition to the standard HF and DFT methods, it is possible to define various approximations which combine elements of both. The simplest of these are the so-called a posteriori methods, whereby the correlation and/or exchange energies are evaluated through integration of exchange-correlation density functionals with the converged HF density:
![]() .
.
Advanced quantum-chemical methods of including correlation effects in CRYSTAL are still under development, and thus the a posteriori DFT correlation-only technique is extremely valuable for the estimation of correlation effects in periodic Hartree-Fock calculations. The method has been examined in detail in references 5 and 6. Results of calculations where the HF exchange energy is subtracted from the total energy, and replaced with both a posteriori correlation and exchange energies have been presented for a set of twenty covalent and ionic solids in reference 7. Finally, one may define a correlation-only Kohn-Sham monoelectronic operator using a combination of the exact non-local HF exchange and a DFT correlation potential,
![]() .
.
This method, which we shall refer to as the hybrid DFT-HF method, was proposed in the original presentation of Kohn and Sham [8] but has not been used even in molecular work until recently [9-11].
The latest version of the CRYSTAL program may thus be used in any of the following modes of operation:
(1) Hartree-Fock
(2) Kohn-Sham DFT
(3) HF + a posteriori DFT correlation
(4) HF + a posteriori DFT exchange/correlation
(5) hybrid DFT-HF
The Coulomb problem
One of the main strengths of the CRYSTAL program is the accuracy of
the treatment of the Coulomb interactions described by the ![]() contribution to the Fock and Kohn-Sham operators. No ‘cut-off’ is introduced
in the evaluation of these interactions in a periodic system, and all the
charge is correctly introduced in the summation of the whole Coulomb series
up to infinity. The sole approximation appears in the transformation of
the infinite series of long-range bielectronic integrals into an infinite
series of monoelectronic integrals, which is evaluated using Ewald techniques.
This transformation is performed via a multipolar analysis of the charge
density, in essentially the same way as in the method that in recent molecular
applications has been referred to as distributed multipolar analysis
or fast multipolar analysis. The use of this technique in the periodic
LCAO scheme has its origin in a very old study of the most efficient multipolar
analysis in small molecules [12] and is documented and analyzed in Ref.
[13]. A complete account of the current treatment of Coulomb interactions
in the CRYSTAL program has been presented elsewhere [14], and only a brief
summary will be given here.
contribution to the Fock and Kohn-Sham operators. No ‘cut-off’ is introduced
in the evaluation of these interactions in a periodic system, and all the
charge is correctly introduced in the summation of the whole Coulomb series
up to infinity. The sole approximation appears in the transformation of
the infinite series of long-range bielectronic integrals into an infinite
series of monoelectronic integrals, which is evaluated using Ewald techniques.
This transformation is performed via a multipolar analysis of the charge
density, in essentially the same way as in the method that in recent molecular
applications has been referred to as distributed multipolar analysis
or fast multipolar analysis. The use of this technique in the periodic
LCAO scheme has its origin in a very old study of the most efficient multipolar
analysis in small molecules [12] and is documented and analyzed in Ref.
[13]. A complete account of the current treatment of Coulomb interactions
in the CRYSTAL program has been presented elsewhere [14], and only a brief
summary will be given here.
Infinite summations of Coulomb terms appear in the electrostatic energy
contribution to the real space Fock and Kohn-Sham matrices. Each matrix
element refers to the interaction of a charge distribution ![]() with the charge density of the whole system
with the charge density of the whole system ![]() :
:
![]() ,
,
where
![]() .
.
The lattice vector 0 refers to the reference cell of the crystal. Similar terms also appear in the evaluation of the Coulomb contribution to the total energy,
![]() ,
,
which corresponds to the interaction of the whole charge density with itself. Note that in the Hartree-Fock Hamiltonian the electron-electron ‘self-interaction’ terms, corresponding to the interaction of each individual electron with itself, are cancelled exactly by equivalent elements of the non-local exchange interaction. However, no such cancellation exists in local exchange density functionals used in the Kohn-Sham Hamiltonian, a fact which has led to well-documented problems in certain systems such as magnetic insulators (e.g. NiO [15]).
The total charge density ![]() can be partitioned into electronic and nuclear contributions, and the various
infinite series involving the different partitions may then be evaluated
independently. In CRYSTAL, the nuclear-electron and nuclear-nuclear terms
are evaluated without approximation using Ewald summation. The electron-electron
Coulomb terms are evaluated using a more complex approximate scheme. The
general contribution to the matrix element may be written as
can be partitioned into electronic and nuclear contributions, and the various
infinite series involving the different partitions may then be evaluated
independently. In CRYSTAL, the nuclear-electron and nuclear-nuclear terms
are evaluated without approximation using Ewald summation. The electron-electron
Coulomb terms are evaluated using a more complex approximate scheme. The
general contribution to the matrix element may be written as
![]() ,
,
where two new lattice vector labels h and l have
been introduced to identify the cells containing the two components of
the ![]() distributions, and P34
is an element of the density matrix (i.e. the direct space representation
of the first-order density operator). The vector sum over the l
lattice vectors converges rapidly, since according to the Gaussian product
theorem the overlap density
distributions, and P34
is an element of the density matrix (i.e. the direct space representation
of the first-order density operator). The vector sum over the l
lattice vectors converges rapidly, since according to the Gaussian product
theorem the overlap density ![]() decays exponentially with increasing separation of the
decays exponentially with increasing separation of the ![]() and
and ![]() functions. By contrast
the h vector sum refers to a long-range interaction which decays
only Coulombically. The resulting series is conditionally and very slowly
convergent and requires an extremely careful analysis. The various infinite
series contributing to each matrix element are therefore limited and approximated
in different ways, as summarized in Fig. 1.
functions. By contrast
the h vector sum refers to a long-range interaction which decays
only Coulombically. The resulting series is conditionally and very slowly
convergent and requires an extremely careful analysis. The various infinite
series contributing to each matrix element are therefore limited and approximated
in different ways, as summarized in Fig. 1.
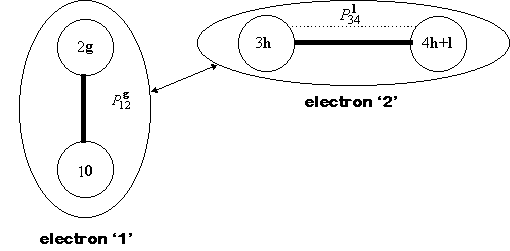
Fig. 1 - Schematic of the Coulomb interaction between distributions. Thick black lines mean 'truncate beyond threshold', the arrowed line means 'approximate beyond threshold'. and the dotted line identifies a density matrix coupling factor.
The bielectronic Coulomb integrals are disregarded completely
when the space integral of either the overlap distribution ![]() or that of the overlap distribution
or that of the overlap distribution ![]() (corresponding to the thick black lines in the figure) is less than a pre-specified
threshold T1. The conditionally-convergent
Coulomb series over h vectors (the arrowed line in Fig. 1) is not
truncated, but is approximated beyond a certain threshold using a distributed
point multipole model of the charge distribution, as follows. The local
basis functions associated with each nuclear site in the reference cell
are partitioned into non-intersecting sets q (‘shells’) sharing
similar asymptotic decay properties. For each shell, the charge density
of an associated shell distribution is then defined according to a Mulliken
partition scheme as
(corresponding to the thick black lines in the figure) is less than a pre-specified
threshold T1. The conditionally-convergent
Coulomb series over h vectors (the arrowed line in Fig. 1) is not
truncated, but is approximated beyond a certain threshold using a distributed
point multipole model of the charge distribution, as follows. The local
basis functions associated with each nuclear site in the reference cell
are partitioned into non-intersecting sets q (‘shells’) sharing
similar asymptotic decay properties. For each shell, the charge density
of an associated shell distribution is then defined according to a Mulliken
partition scheme as
![]() .
.
This definition saturates the {4,l} indices of the basis
function (chi4,h+l), and allows the conversion of many four-centre bielectronic
integrals between overlap distributions into a single three-centre integral
between an overlap distribution and a shell distribution. The list of h
vectors is partitioned into a finite internal set {hbi}
and an infinite external set {hmono} for each ![]() ,
using overlap criteria and a second penetration threshold T2.
The electron-electron Coulomb contributions to the Fock matrix may then
be split into internal and external terms:
,
using overlap criteria and a second penetration threshold T2.
The electron-electron Coulomb contributions to the Fock matrix may then
be split into internal and external terms:
![]() .
.
The bielectronic part is calculated through explicit evaluation of the four-centre bielectronic integrals I(12g;34l), to give
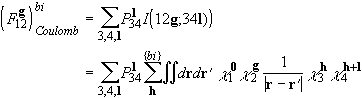 .
.
The monoelectronic term, which involves an infinite sum of Coulomb
integrals involving electronic distributions that are ‘external’ to each
other, is calculated in an approximate way. The potential at a field point
![]() due to each shell distribution
due to each shell distribution
![]() is given to a good approximation
by the spherical multipolar expansion
is given to a good approximation
by the spherical multipolar expansion
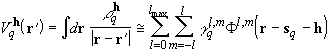 .
.
Here ![]() is the l,m
multipole of the shell charge distribution centred at
is the l,m
multipole of the shell charge distribution centred at ![]() (the position of the function
(the position of the function ![]() in cell h), and the field term
in cell h), and the field term ![]() represents the potential at the point r due to an infinite array
of unit point multipoles
represents the potential at the point r due to an infinite array
of unit point multipoles ![]() . Note
that the multipolar expansion is truncated at some maximum value lmax.
(which may be up to six). With this approximation, the external Coulomb
contribution to the Fock matrix may be rewritten as
. Note
that the multipolar expansion is truncated at some maximum value lmax.
(which may be up to six). With this approximation, the external Coulomb
contribution to the Fock matrix may be rewritten as
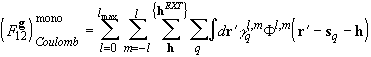
where the sums over h in the field terms are treated using Ewald techniques. This approximate scheme produces a speed up of around an order of magnitude and lowers considerably the amount of disk space required, with little or no loss of accuracy with respect to an ‘exact’ scheme.
Many different strategies have been used in both molecular and periodic ab initio LCAO calculations for the ‘analytical’ treatment of the Coulomb interaction. Often an auxiliary basis set is used to fit the electronic density (and thus the electrostatic potential) and then the matrix elements are evaluated analytically as three-centre integrals [16]. In the most recent literature however, particular emphasis has been placed on approximate analytical methods similar to those used in CRYSTAL based on a multipolar analysis of the long-range interactions [17]. The wider debate concerning techniques and the method of charge partitioning for defining the multipoles is currently of great interest.
Numerical integration techniques
We have seen that the contribution to the total energy of electron-electron interactions beyond the one-electron Coulomb term is evaluated by an integral of the type
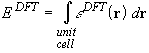 ,
,
where ![]() is the DFT energy
density representing exchange-correlation or correlation-only interactions.
If all-electron basis sets are used, the integrand has very pronounced
cusps corresponding to nuclear positions since the correlation energy density
is roughly proportional to the electron density
is the DFT energy
density representing exchange-correlation or correlation-only interactions.
If all-electron basis sets are used, the integrand has very pronounced
cusps corresponding to nuclear positions since the correlation energy density
is roughly proportional to the electron density ![]() and the exchange energy density is roughly proportional to the four-thirds
power of
and the exchange energy density is roughly proportional to the four-thirds
power of ![]() . Where effective-core
pseudopotentials are used, the pseudo-density in the core region may also
show similar features. A numerical integration method capable of taking
into account the cusp-shaped nature of the integrand functions is thus
required. This precludes, for example, use of the homogeneous sampling
methods [18] applied in LCAO crystalline calculations to numerically integrate
reciprocal space quantities, which cannot be applied in the integration
of such highly inhomogeneous quantities defined in direct space. We have
therefore chosen to use the atomic partition method, originally
applied by Becke [19] and Savin [20] to molecular systems. In this method,
atomic domains are defined over which one performs spherical integrations
that concentrate many sampling points in the core cusp region. Naturally,
the atomic domains overlap each other and the necessity of avoiding border
discontinuities complicates the numerical quadrature. Furthermore, the
application of these methods to periodic systems requires some modification
and careful calibration.
. Where effective-core
pseudopotentials are used, the pseudo-density in the core region may also
show similar features. A numerical integration method capable of taking
into account the cusp-shaped nature of the integrand functions is thus
required. This precludes, for example, use of the homogeneous sampling
methods [18] applied in LCAO crystalline calculations to numerically integrate
reciprocal space quantities, which cannot be applied in the integration
of such highly inhomogeneous quantities defined in direct space. We have
therefore chosen to use the atomic partition method, originally
applied by Becke [19] and Savin [20] to molecular systems. In this method,
atomic domains are defined over which one performs spherical integrations
that concentrate many sampling points in the core cusp region. Naturally,
the atomic domains overlap each other and the necessity of avoiding border
discontinuities complicates the numerical quadrature. Furthermore, the
application of these methods to periodic systems requires some modification
and careful calibration.
The partitioning of space into overlapping atomic domains is achieved through the definition of weight functions wA(r) for each nucleus A such that, for all r,
![]() .
.
Each weight function has a value of unity near its own nucleus and vanishes in a continuous and well-behaved manner near any other. The multi-centre integration may then be decomposed into a sum of single-centre atomic integrations over each of the nuclei of the system. To satisfy the condition of Eq. 27, each weight function must be normalized according to
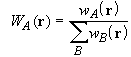 .
.
The integration space of the atomic integrals is over all space,
but the integrand function ![]() has a cusp in the position of atom A, and goes rapidly to zero in
the direction of the other atoms.
has a cusp in the position of atom A, and goes rapidly to zero in
the direction of the other atoms.
In the Becke atomic partition scheme [19], the weight functions ![]() are defined as
are defined as
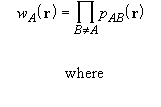
![]()
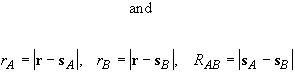
The confocal elliptical coordinate ![]() defines a projection of the point
defines a projection of the point ![]() along the vector
along the vector ![]() , that connects
atoms A and B. The function
, that connects
atoms A and B. The function ![]() is some kind of step function, equal to unity at the position of atom A
and equal to zero at atom B. The product of the functions
is some kind of step function, equal to unity at the position of atom A
and equal to zero at atom B. The product of the functions ![]() for all pairs
for all pairs ![]() thus defines
a polyhedron around atom A, with the weight function
thus defines
a polyhedron around atom A, with the weight function ![]() equal to one inside the polyhedron, and zero outside. These Voronoi polyhedra
fill all of space. In practice, smoothed step functions
equal to one inside the polyhedron, and zero outside. These Voronoi polyhedra
fill all of space. In practice, smoothed step functions ![]() are used, where the weight function
are used, where the weight function ![]() goes continuously to zero outside the polyhedra; this avoids numerical
integration problems, but the calculation must be extended beyond nearest
neighbour AB pairs if high accuracy is desired.
goes continuously to zero outside the polyhedra; this avoids numerical
integration problems, but the calculation must be extended beyond nearest
neighbour AB pairs if high accuracy is desired.
The calculation of the normalized weight functions ![]() using the Becke method requires the evaluation of sums of products of pair
functions, and has a relatively high computational cost in large molecules
and condensed systems. As an alternative, simpler weights can be defined,
such as those suggested by Savin [20]:
using the Becke method requires the evaluation of sums of products of pair
functions, and has a relatively high computational cost in large molecules
and condensed systems. As an alternative, simpler weights can be defined,
such as those suggested by Savin [20]:
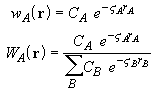 .
.
These weight functions are simple exponential functions which
roughly mimic the electronic density around atom A. The exponential
is normalized to coincide with the number of electrons associated with
atom A according to a Mulliken analysis, and the exponent coefficient
![]() is defined to reproduce the
atomic shape, taking into account the atomic or ionic dimension. The evaluation
of the weight WA requires only the
summation of exponential functions centred on the neighbours of atom A.
This method can be applied to very complex molecules and crystals, and
the loss of accuracy is less than one order of magnitude with respect to
the Becke scheme. Both Savin and Becke weights have been implemented in
the new version of the CRYSTAL program.
is defined to reproduce the
atomic shape, taking into account the atomic or ionic dimension. The evaluation
of the weight WA requires only the
summation of exponential functions centred on the neighbours of atom A.
This method can be applied to very complex molecules and crystals, and
the loss of accuracy is less than one order of magnitude with respect to
the Becke scheme. Both Savin and Becke weights have been implemented in
the new version of the CRYSTAL program.
We must now consider how to extend the atomic partition method to a periodic scheme. In periodic systems the integration is confined to the unit cell, which is a finite polyhedron in 3D periodic systems (crystals), a polyhedron infinite in one dimension in 2D systems (slabs) and a cylinder with infinite radius in 1D systems (polymers). The same transformation from one multi-centre integral to a sum of atomic integrals can be performed as in molecules, but infinite lattice sums arise in the evaluation of the normalized weight functions,
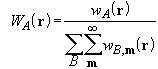 .
.
The expression for the exchange-correlation energy is thus
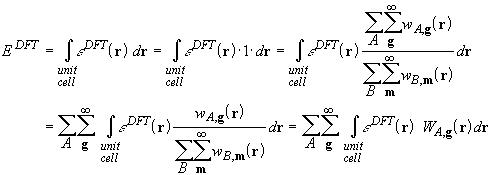 .
.
Since the integrand functions are invariant under lattice translations,
![]()
![]() ,
,
a translation of the coordinate ![]() may be applied to each integral:
may be applied to each integral:
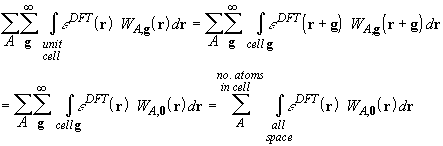
In this way, the infinite lattice sum of unit cell integrals is transformed into a space integration strictly analogous to the molecular case. The weight W contains a lattice sum, which can be truncated using various techniques. With the exponential weight functions of Savin, the lattice sums are truncated when the exponentials are smaller than a given threshold Tw. In 0-, 1-, and 2-dimensionally periodic sytems however, there are regions far from all atomic centres, where the limit of W is finite:
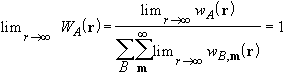
In such regions the electron density (and functionals thereof) decay exponentially, and thus very small thresholds must be used for an acceptable accuracy in the integrated charge.
The treatment of the lattice sums is more complex when Becke weight
functions are employed. The ![]() weights, defined in Eq. 29, are products of a finite set of functions
weights, defined in Eq. 29, are products of a finite set of functions ![]() which are defined for each neighbour B within a certain ‘cutoff’
distance
which are defined for each neighbour B within a certain ‘cutoff’
distance ![]() of atom A.
If a step function is used in the definition of
of atom A.
If a step function is used in the definition of ![]() such that the resulting Voronoi polyhedra have sharp boundaries, only the
first neighbours of A need be taken into account. Because of the
difficulty of finding an efficient quadrature for a step function, a ‘smoothed’
cutoff function
such that the resulting Voronoi polyhedra have sharp boundaries, only the
first neighbours of A need be taken into account. Because of the
difficulty of finding an efficient quadrature for a step function, a ‘smoothed’
cutoff function ![]() is actually
more convenient. We use an odd polynomial obtained by iterating the function
is actually
more convenient. We use an odd polynomial obtained by iterating the function
![]() ,
,
according to
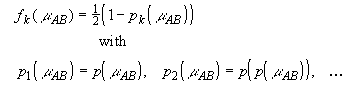
Three iterations (i.e. k = 2) of Eq. 37 generate a ninth-degree
polynomial which Becke has shown to be of optimum form for molecular calculations
[19]. In tests on three-dimensional periodic systems however, we have found
that a sixth degree polynomial generated by just two iterations gives more
accurate results. This difference is presumably related to the higher average
coordination of atoms in the solid state and the consequent larger number
of vertices in the Voronoi polyhedra. The current version of the code thus
switches between the different cutoff functions according to the dimensionality
of the calculation. The shape of the smoothed cutoff function allows the
lattice sum of weights ![]() appearing
in the denominator of Eq. 31, which is in principle infinite, to be limited
to a set of atoms within some distance
appearing
in the denominator of Eq. 31, which is in principle infinite, to be limited
to a set of atoms within some distance ![]() of atom A. The question of appropriate values for the two parameters
of atom A. The question of appropriate values for the two parameters
![]() and
and ![]() will be addressed in the following section.
will be addressed in the following section.
Many quadrature techniques exist to evaluate one-dimensional integrals [21], but the numerical evaluation of multi-dimensional integrals is less common, and is usually done using direct products of one-dimensional quadratures. In our case, the most efficient numerical integration method exploits the atomic, quasi-spherical shape of the integrand by introducing spherical coordinates to separate the radial and angular integrations,
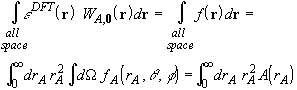
where ![]() is the radial
distance of the sampling point from the nucleus A, and A(rA)
is the value of the angular integral at r = rA.
Two-dimensional quadrature on the surface of a sphere has been fully developed
by Lebedev [22], who derived very efficient sets of sampling points and
weights. His richest set of 435 points is able to integrate exactly a 35-degree
polynomial in the angular coordinates
is the radial
distance of the sampling point from the nucleus A, and A(rA)
is the value of the angular integral at r = rA.
Two-dimensional quadrature on the surface of a sphere has been fully developed
by Lebedev [22], who derived very efficient sets of sampling points and
weights. His richest set of 435 points is able to integrate exactly a 35-degree
polynomial in the angular coordinates ![]() .
This is enough to integrate exactly functionals of the atomic density with
angular quantum numbers of up to l = 6 and m = 6 (i.e. i
functions) and hence allows high accuracy for any atomic coordination.
The octahedral symmetry of the Lebedev grids confers the additional advantage
of a straightforward selection of irreducible set of points using the local
symmetry of each atomic site. By contrast, sampling techniques in
.
This is enough to integrate exactly functionals of the atomic density with
angular quantum numbers of up to l = 6 and m = 6 (i.e. i
functions) and hence allows high accuracy for any atomic coordination.
The octahedral symmetry of the Lebedev grids confers the additional advantage
of a straightforward selection of irreducible set of points using the local
symmetry of each atomic site. By contrast, sampling techniques in ![]() based on one-dimensional quadrature cannot fully exploit the local symmetry,
which is an important consideration in condensed systems. The expression
for the angular integral A(rA)
is thus
based on one-dimensional quadrature cannot fully exploit the local symmetry,
which is an important consideration in condensed systems. The expression
for the angular integral A(rA)
is thus
![]() ,
,
where w i are the Lebedev weights.
We have examined various ways of performing the radial integration. Standard one-dimensional Gaussian quadrature techniques were found to be appropriate [23]. The most critical region of the integration is in the vicinity of the nucleus, where the integrand functions, which are functionals of the electron density, have cusps that span several orders of magnitude. As a result, large numbers of orthogonal polynomials are necessary for accurate Gaussian quadrature, and therefore a high number of sampling points are required in the calculation. It is possible to subdivide the integration region into segments, with a separate numerical quadrature for each segment allowing the concentration of points in the core region. In practice however, we have found that the shape of the integrand in our application means that little computational advantage is afforded by this procedure, and we therefore use only a single radial interval. The most critical point is simply the number of orthogonal polynomials in the quadrature. The one-dimensional numerical integration of a function between limits of zero and infinity can be performed using the weights and the nodes of polynomials orthogonal to an exponential weight function, such as the Laguerre polynomials. However, we have found it more convenient to use polynomials orthogonal on a finite interval, with the finite intervals mapped onto an infinite interval by means of an opportune transformation of the coordinates,
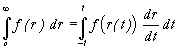 .
.
A logarithmic transformation of the coordinates allows the Gauss-Legendre quadrature to be used for an integration with an infinite upper limit,
![]() .
.
The Gauss-Legendre radial quadrature was found to be more accurate than either the Gauss-Laguerre or other techniques proposed in the literature, such as the Euler-McLaurin and Gauss-Chebyshev methods.
Different levels of accuracy for the angular integration may be used for different values of the radius by varying the number of sampling points on the surface of the sphere, and the number of angular points as a function of the radius must therefore be optimized for an efficient implementation of the scheme. In general, the angular accuracy may be decreased in the region of the nucleus, since the electronic density and functionals thereof become spherically symmetric as the radius of the sphere tends to zero.
An appropriate set of points for spherical quadrature can be defined by the degree L of the angular polynomial that can be integrated exactly. Lebedev octahedral grids may be used only up to L = 35, and so for L > 35, it is convenient to use a product formula involving the direct multiplication of a Gauss-Legendre quadrature in q by a ‘trapezoidal’ quadrature in f with equally spaced points. Nq times 2Nf points may then be used to exactly integrate spherical polynomials of Nth degree. Many scaling criteria have been tested for the angular degree L with the result that power, logarithmic and exponential functions L(r) gave less accurate results than the following simple linear scaling [24],
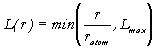 .
.
where Lmax is a pre-defined maximum degree of polynomial that can be integrated exactly. The function L(r) thus increases linearly with r up to a value rmax, where its gradient changes discontinuously and the function assumes a constant value equal to Lmax. If the angular degree L is less than 35 at a particular radial point, then the next larger Lebedev grid is adopted, so that L is varied discontinuously in the set 9, 11, 17, 23, 27, 29, 35. If L is greater than 35, CRYSTAL uses the Legendre-trapezoidal grids with a maximum angular degree of L = 60.
Results
The paramount but conflicting issues in assessing the performance of the new code are necessarily accuracy and computational cost. Highly accurate numerical integrations lead to a substantial increase in CPU time, and so it is important that the accuracy is under the control of the user, but in as transparent a way as possible. The space of internal parameters that control the numerical integration process has therefore been calibrated, and the results of the calibration used to define a minimal set of user-definable computational parameters. The dependence of various calculated observables on these parameters may then be used to define their default values. This process will now be discussed in detail.
The use of the linear scaling of the angular degree L(r) discussed in the previous section simplifies the parameter space to be optimized. Given that the radial integration is performed on a single infinite interval over a number of points R, then a simultaneous variation of both R and Lmax may be made. Optimum pairs of values may be selected to minimize the error for a given number N of grid points per atom. Since the same criteria must be applied to both periodic (crystals, slabs and polymers) and non-periodic systems (atoms and molecules), we have used a set of eighteen systems in the calibration including closed and open-shell atoms, molecules, polymers, slabs, and covalent, semi-ionic and ionic crystals. Table 1 identifies these systems and the basis sets used. For atoms and molecules we use various standard sets, while those for the crystalline calculations have a similar structure to standard molecular sets such as STO-3G and 6-21G [25] and we thus employ the same notation. The crystalline sets used are published in references 26 and 27.
A convenient way of assessing the accuracy of the DFT energy integration,
and hence of selecting the optimum computational conditions, is given by
the charge density integration. We define the relative error D
as the error in the integrated charge with respect to the actual number
of electrons (per unit cell for periodic systems). This may conveniently
be expressed in parts per million (ppm). The relative error in the integrated
charge averaged in the mean over the eighteen test systems, ![]() ,
may be used to discuss the influence of the computational parameters on
the integration accuracy. The set of parameters was subdivided into homogeneous
subsets of angular parameters, radial parameters, and weight parameters.
Each subset was then varied in turn, beginning from a basic set of parameters
given by a previous optimization.
,
may be used to discuss the influence of the computational parameters on
the integration accuracy. The set of parameters was subdivided into homogeneous
subsets of angular parameters, radial parameters, and weight parameters.
Each subset was then varied in turn, beginning from a basic set of parameters
given by a previous optimization.
A large number of tests for each of the systems in Table
1 were carried out to determine the average error in the integrated
charge ![]() and the cost of the
calculation C for many pairs of values of R and Lmax.
For a machine-independent estimate of C, the cost was assumed to
be proportional to the the number of grid points per atom (without taking
symmetry into account). A contour plot of
and the cost of the
calculation C for many pairs of values of R and Lmax.
For a machine-independent estimate of C, the cost was assumed to
be proportional to the the number of grid points per atom (without taking
symmetry into account). A contour plot of ![]() as a function of R and Lmax
is shown in Fig. 2. This data was used to derive a function
as a function of R and Lmax
is shown in Fig. 2. This data was used to derive a function ![]() max(R)
which, for each R, gives the lowest value of Lmax
for which the integration error
max(R)
which, for each R, gives the lowest value of Lmax
for which the integration error ![]() is a minimum. From
is a minimum. From ![]() max(R)
and C(R, L) follows the function D
min(C), which gives the smallest
average error for a given number of grid points per atom, and this is plotted
in Fig. 3. This relation simplifies enormously the choice of predefined
sets of grid parameters.
max(R)
and C(R, L) follows the function D
min(C), which gives the smallest
average error for a given number of grid points per atom, and this is plotted
in Fig. 3. This relation simplifies enormously the choice of predefined
sets of grid parameters.
[Fig. 2, Fig 3 no longer available - see the paper]
Finally, the stability of the results with respect to variation of the cutoff radii BS and BP for sums and products of Becke weights was investigated using the set of eighteen test cases; values in the range 6 to 9 Å for both parameters were found to give converged results.
These results have been used to define three user-definable computational parameters, which control the numerical integration of the total energy, the numerical integration of the Kohn-Sham matrix elements and the properties of the auxiliary basis set. These will now be described. The first two parameters alter the accuracy of the numerical integrations through the use of different types of weight function, variation in the number of radial and angular sampling points and variation of the Becke cutoff radii BS and BP. Identical values of the various internal variables are used to define both parameters and these are summarized in Table 2.
The quality of the auxiliary basis set may be varied using a third parameter, whose effects are summarized in Table 3.
Although the values of the three computational parameters are under the control of the user, it is important to define default settings offering a reasonable compromise between accuracy and cost, since the details of the numerical integration will be unimportant to the average user. For this purpose we now give detailed results for three cubic test systems: a covalent crystal (silicon), an ionic crystal (sodium chloride) and a metal (aluminium). Reasonably high quality basis sets (6-21G* for Si, 8-31G for Al, 8-511G for Na and 86-311G for Cl) were used. The reciprocal space integration necessary to reconstruct the Kohn-Sham matrix in direct space was performed by sampling the Brillouin zone at a regular set of points defined by shrinking factors of 8 (NaCl, Si) and 16 (Al) [1,18] which were sufficient to give convergence in the three cases. The calculations were performed using standard LDA density functionals, namely Dirac-Slater exchange and Perdew-Zunger correlation [Appendix 1]. In Table 4, Table5 and Table6, the variation of the calculated lattice parameters, bulk moduli, atomization/ionization energies and total energies are given for each of the possible values of the three computational parameters. Note that in order to reduce the amount of information, a prior knowledge of the three default settings is assumed in the tables, and each parameter is varied holding the other two at their default value. Gaps in the tables refer to situations where a parameter was too low for a sensible answer to be obtained.
For each crystal the results are seen to converge at a sufficiently high value of the computational parameter. The results are most sensitive to the parameter which controls the numerical integration of the total energy, they are fairly sensitive to the quality of the auxiliary basis set, and depend hardly at all on the accuracy of the matrix element integration. For the highest value of the accuracy of the total energy integration, the lattice parameters are –0.4% (silicon), –1.2% (aluminium) and –1.3% (sodium chloride) smaller than the experimental value. The values for the bulk moduli are in error by +1.8% (silicon), +2.1% (aluminium) and +18.6% (sodium chloride). The converged results are comparable in accuracy with the results of other studies using different methods and plane-wave basis sets (Table 7). We conclude that the calculation of the density functional self-consistent potential does not need a particularly high accuracy: integration errors of 100 ppm are acceptable, corresponding to 4000 points per atom for the systems studied. The density functional energy calculation requires an accuracy of at least 10 ppm (10000 points per atom) and possibly even higher if elastic properties are to be computed.
As a further check, we examine the calculated band structures, shown in Figs 4 (a-c) [not available -see the published paper] between selected k-points for Si, Al and NaCl. While these show relatively good agreement with other calculations in the literature, detailed interpretations of the various features of the band structures are irrelevant at this stage, and we concern ourselves merely with changes in the eigenvalue spectrum as a function of the various computational parameters. Table 8 reports the numerical values of the direct and indirect band gaps of the silicon eigenvalue spectrum, together with the valence band width, as a function of computational parameters 2 and 3 (the details of the band structure do not, of course, depend on the accuracy of the total energy integration controlled by parameter 1). All three quantities show relatively little dependence on the accuracy of the matrix element integration, but the effect of the quality of the auxiliary basis set is not negligible. In particular, four atom-centred s functions were insufficient to open a gap in the spectrum and a metallic solution was obtained. Changing the auxiliary basis set parameter from 1 to 3 decreased the valence band width by 0.35 eV, and increased the direct and indirect gaps by 0.7 eV and 0.75 eV respectively. Similar trends were observed for other materials.
On the basis of the results presented in this section, and in particular those of Tables 4, 5 and 6, default values for the computational parameters may be defined. Reasonable compromises between accuracy and cost are 3 for the total energy integration (parameter 1), 2 for the matrix element integration (parameter 2) and 2 for the quality of the auxiliary basis set (parameter 3).
Finally, a comparison of various properties of three simple molecules and their constituent atoms computed using both CRYSTAL and the well-established GAUSSIAN 94 package [39] is given in Appendix 2. Equivalent 6-31G* basis sets were used in both sets of calculations, and the CRYSTAL numerical integration parameters were set at 4, 4, and 3 for the total energy integration, matrix element integration and auxiliary basis set controls respectively. The two codes are seen to give essentially equivalent results for the bond lengths, bond angles and atomization energies of CO, H2O and CH4. While further tests are obviously necessary, particularly with regard to the influence of the auxiliary basis set, the current implementation of density functional theory in the CRYSTAL code thus appears to be stable and gives results essentially in agreement with experiment and other theoretical calculations. Further work is currently in progress to test the code as widely as possible on more complex systems.
Conclusion
In this paper we have given an overview of the algorithms used in the introduction of the density functional theory into the computer code CRYSTAL, with particular emphasis on the problem of numerical integration. The scheme was tested on various representative materials, and the results used to derive a set of computational parameters through which the accuracy and cost of the calculation may be transparently user-defined.
Acknowledgements
MDT acknowledges the European Commision for the award of a fellowship under the Human Capital and Mobility Scheme, contract no. ERBCHICT941605. MC would like to thank the Consiglio Nazionale delle Ricerche for financial support. AZ would like to thank the Slovenian Ministry of Science and Technology for financial support of his Ph.D. studies.
References
This article was created from a Microsoft Word document, a program which several years ago I was stupid enough to use. The references were formatted as footnotes, which naturally it is unable to convert to HTML. Sorry. Use LateX to write papers at all times - it doesn't have a dancing paperclip.