12. NiO: LSDA case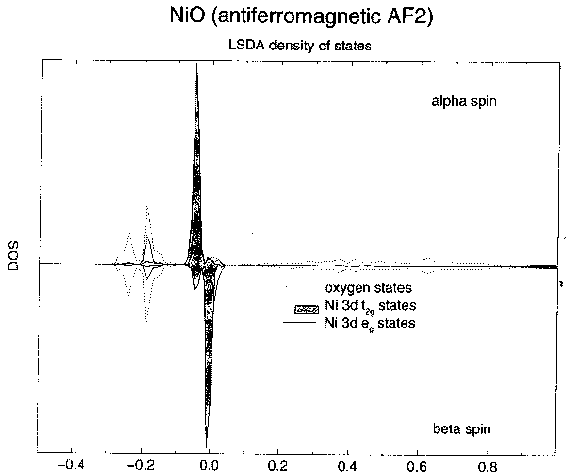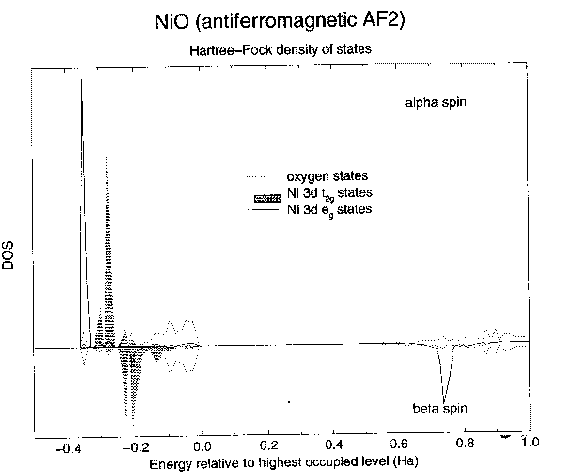

The problem is in fact specific to density functional theory, as I will now demonstrate. One would normally imagine that DFT is better than Hartree-Fock, because DFT includes electron correlation. This is true. However, that isn't really the issue here (surprisingly) as we will now see.

It happens that the program I'm using can do DFT calculations as well. This is good because it means I can do a calculation with the same basis set, the same computational algorithms and the same level of accuracy as we did before. Any differences that we see will then be purely due to the Hamiltonian that we use. Well, let's do an LSDA calculation - what do we get? Answer, see the DOS plot above.

This is a metal. Look where the Fermi level is. It's right in the middle of the d states. Look where the Fermi level is in the Hartree-Fock case - right at the top of the oxygen bands. Now, when this happens, people often point out that everybody knows that the LDA underestimates band gaps - so if we can magically increase the band gap, everything will be alright. This is not a correct statement of the problem however. Look at what we have here. We know what the DOS should look like. Everything is wrong. The only thing splitting the d states here is the exchange; the majority spin bands are slightly lowered with respect to the minority spin bands. If there are more electrons with my spin, then I can lower my energy more by avoiding them.

The important point is that the whole Mott-Hubbard idea of different potentials for occupied and unoccupied d orbitals has gone out of the window. The one-electron potential is no longer orbital dependent. We don't have any orbital polarization. The LSDA is apparently not capable of producing a different potential for different d orbitals with the same spin.

And to add to the misery, well, we know quite clearly from experiment that the oxygen states have to lie at the top of the valence band. NiO is a charge transfer insulator. But here they are 8 eV below where they should be. It's as if the whole 3d manifold has been shoved up in energy by some spurious interaction. And as we'll see, that's precisely what has happened.