14. Self-interaction in DFT

  • e-e Coulomb (Hartree) term:

  • Apply to one-electron system with wave function

  • In DFT (LSDA) we add the exchange correlation energy to work out electron-electron interaction energy

  • Exact exchange-correlation energy functional would cancel the self-interaction. The L(S)DA doesn't.




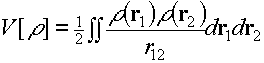
So what exactly is the problem with these DFT calculations? The problem is related to self-interaction, which as its name suggests, is the spurious interaction of an electron with itself. In Hartree-Fock, self-interaction is explicitly and exactly cancelled, which is why it appears to work. With the LDA, self-interaction is not cancelled. This is not good.

Every term in the Kohn-Sham Hamiltonian is a functional of the density. The electron-electron Hartree interaction looks something like the second equation above. This is similar to the Hartree-Fock Coulomb integral we saw earlier - we just take our pair of little boxes in all possible positions in space and form a weighted sum of the interactions to give the total Coulomb energy. You can see there is a self-interaction because this expression is not zero for a one electron system. Take some position r1, and some other position r2, the density is not zero at either point so the integral is not zero.

When we do a local spin density approximation we add an exchange correlation energy, like the fourth equation above. If we knew the exact DFT exchange-correlation functional, then the self-interaction would be cancelled, but we don't and it isn't. I'll show you what this means for strongly correlated systems in a moment. First, let's just establish that this problem doesn't arise in Hartree-Fock..