15. Self-interaction in HF

  • Hartree-Fock case: label orbitals: occupied (a,b,...) and virtual (i,j,...). What is the expression for the orbital energy?

  • Sum is over occupied orbitals only. For the first expression only, one of the terms will cancel.

  • Therefore in the HF approximation an electron does not feel its own field, since the self-interaction is cancelled by an equivalent term in the exchange energy.



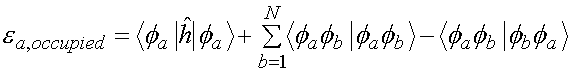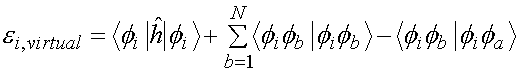
Self-interaction is explicitly cancelled in Hartree-Fock. Why?.

Let's write down expressions for the occupied and virtual orbital energies. Each contains a one-electron term (KE plus interaction with external potential) which is not relevant to the current argument. It also contains a Coulomb interaction and an exchange interaction of opposite sign. The sum over b is over all N electrons i.e. over all the occupied orbitals. Self-interaction happens when b=a. When that is the case, the Coulomb interaction of an electron with itself is cancelled by an equivalent term in the exchange energy. Hence no self-interaction. The non-local character of the exact exchange term therefore takes into account the different nodal structures of the orbitals. It's important to notice that the potential for occupied and unoccupied orbitals is different. Because i is never equal to b, a virtual or unoccupied orbital feels the potential of N electrons. an occupied orbital feels the potential of N-1 other electrons. And so you see that the correct Mott-Hubbard physics depends quite precisely on the explicit cancellation of the self-interaction.