18. Self-interaction corrections and localization

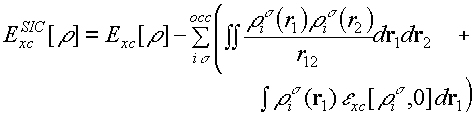Well, we've seen that for NiO the HF approximation 'works', to a certain extent, and normal DFT doesn't. In many ways however, Hartree-Fock is a rather poor approximation, because it doesn't have a correlation term. So if DFT could be made to work, obviously we would prefer to do that. Is there anything that we can do about the self-interaction problem, for example? Yes - in DFT you can write down a correction for this very easily.

We sum over the occupied Kohn-Sham orbitals from which we get the density and we subtract the Coulomb energy of an electron in each orbital interacting with itself. We also subtract the spurious E_xc contribution that we get by feeding in the density of a single spin orbital, i.e. one of the spin densities that E_xc depends on will be zero.

This may seem straightforward, but there is a problem. We now have orbitals appearing, where previously we only had densities. And this 'SIC correction' actually depends on which orbitals we choose to self-interaction correct - i.e. the total energy is no longer invariant to a unitary transformation of the occupied orbitals among themselves. So if we start with delocalized Bloch orbitals, we can form some linear combinations and convert them into localized orbitals, and the total energy of a SIC LDA calculation will change.

Now, let's think about localization for a minute. We've been saying, without really defining what we mean, that the electrons in strongly correlated systems in a Mott insulator are localized. Do we see that in a Hartree-Fock calculation? Well, at first sight, no. The canonical crystalline orbitals which are the solutions to the Hartree-Fock equations are delocalized throughout the entire crystal. What does that imply about localization of electrons? Nothing really. Here's a noddy argument: each orbital has an associated wave vector k, so what we've done is to localize it precisely in momentum space, which from the uncertainty principle you might say, means that we're completely uncertain about its position. You can then do a unitary transformation, take linear combinations of the orbitals at various different k to form Wannier functions, which localize the electron to a greater or lesser extent in real space, and we're less certain about momentum.The point about HF is that the energy is completely invariant to a unitary transformation, so carrying out this mixing doesn't tell us anything at all. There is no criterion for saying which unitary transformation. It's completely arbitrary.

There are ways you can define what you mean by electron localization, and they can be defined in something as simple as Hartree-Fock. See recent work by Bader, Andreas Savin (the 'electron localization function' or ELF), Raffaele Resta and others.

The point is that for a completely delocalized Bloch orbital in an infinite system the self-interaction correction defined by this formula is zero, because the density of a single electron in that orbital goes as 1/N where N is the number of electrons in the system. We can then make any arbitrary unitary transformation to make the orbitals more localized and the energy will change. So which set of orbitals do you choose? Well, what people have generally done is to pick the set of orbitals that minimize the energy. And in that case everything becomes quite hard. The variational minimization of the energy is no longer an eigenvalue problem in a self-consistent potential - you have to use things like steepest descents and other minimization methods and so this is actually a very hard thing to do.. [Quite a lot of people do this, however]

The 'hybrid' functionals currently popular in quantum chemistry will do quite well for many-strongly correlated materials because the proportion of exact Hartree-Fock exchange that they contain allows an orbitally-dependent potential to be produced.