19. KCuF₃ - I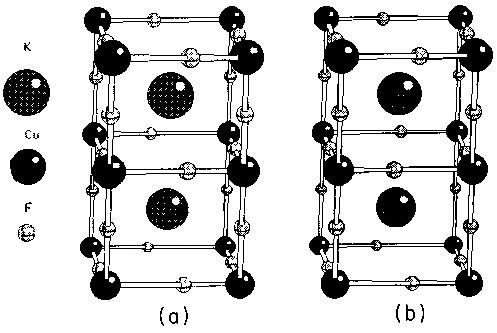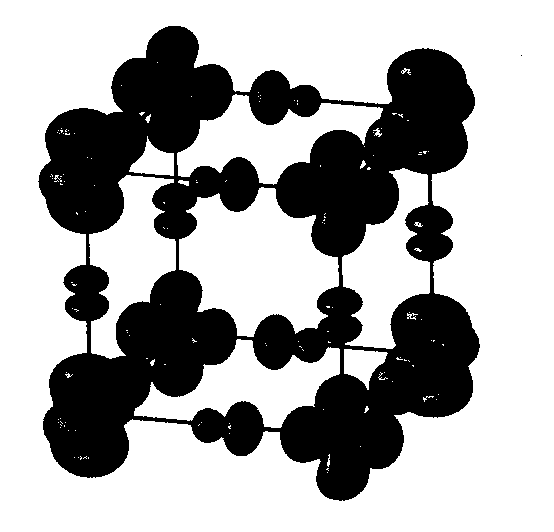

So, enough theory. Let's head off on a tour of strongly correlated systems and see what interesting phenomena we can look at. First, co-operative Jahn-Teller effects, orbital ordering and magnetism..

Potassium copper trifluoride is rather a nice system. It's a perfect test case for seeing what we can do with magnetism. Let's see why. Aboce you can see the crystal structure. It's a perovskite. You have a series of cubes with copper at the corners and non-magnetic fluoride ions in the middle of the bonds. You have a big inert potassium ion sitting in the middle of the cube which will be of no further interest. The first thing that you should note is that it is pseudocubic, in the sense that the distance between magnetic copper ions along the three cubic axes is almost the same.

And yet, consider this. Along the c-axis here [i,e, VERTICALLY UPWARDS IN THE PICTURE], we have a very strong antiferromagnetic superexchange interaction like in NiO with a coupling constant of 200 K. And yet along the axes perpendicular to that the magnetic interaction is virtually non-existent. In fact it's slightly ferromagnetic with a coupling constant of 2K, two orders of magnitude smaller. So in fact this is essentially a one-dimensional magnet. You just have one-dimensional antiferromagnetic strings running up the c-axis which hardly interact magnetically at all with adjacent strings. Why? What's going on? Well, I'm cheating slightly, because I haven't told you that this crystal is Jahn-Teller distorted. So the strange magnetic properties are to do with a rather subtle interplay of the superexchange interactions with a cooperative Jahn-Teller effect. The fluoride ions in the basal plane here are actually not sitting in the middle of the bonds. Because Cu2+ is a Jahn-Teller ion, the octahedra distort to break the electronic degeneracy.

When this happens you see the phenomenon known as 'orbital ordering' where the shape of the charge density on the Cu ions orders to minimize electrostatic repulsion. Cu is a d9 ion - it has 'one hole'. What we see in the second diagram above is a plot of the spin density in three dimensions. The unpaired spin roughly corresponds to the position of the 'hole' and you can see that it's orientation changes from one Cu ion to the next.