3. Example: the 3d monoxides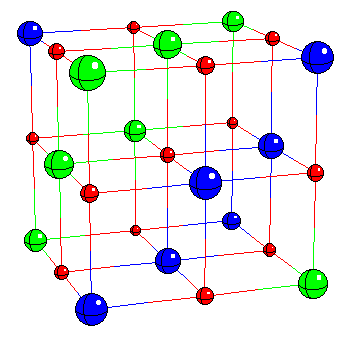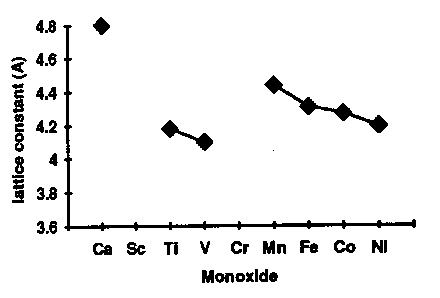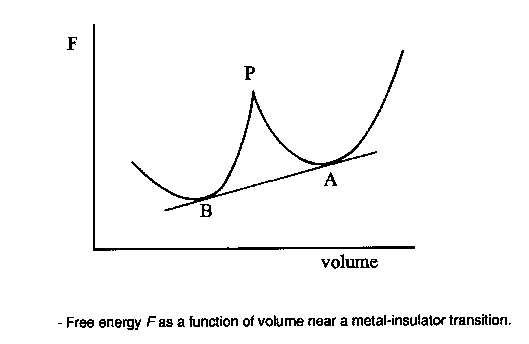

If we want a framework in which to discuss the problem then, we could do worse than to choose NiO and the other 3d monoxides. Later I'll show you the results of calculations for lots of more complicated systems, such as hight Tc materials, but these monoxides are in principle so simple that they represent an ideal test bed. All these things have the same rock salt crystal structure, which looks like this [FIRST PICTURE ABOVE] apart from CuO; Cu2+ is a Jahn Teller ion so the structure distorts into something fairly hideous. Now, imagine the FIRST PICTURE is NiO: the red ions are oxygens, the blue and green ions are both nickel, but blue and green corresponds to different spins, so youre seeing the antiferromagnetic sublattice. You have planes of opposite spin alternating up the [111] body diagonal. Every up spin nickel has six down spin neighbours, and so on. This is because the main magnetic interaction is this antiferromagnetic 180 degree superexchange contact between two magnetic ions via an intervening non-magnetic anion, of which more later.

Actually you see something like a Mott transition as you go across the series [SECOND PICTURE]. The ones at the right here are all antiferromagnetic Mott insulators, and have very similar properties, but as we progress to the left the nuclear charge decreases, the orbitals expand, leading to more overlap, an increase in the band width, and tendency to delocalize, and so by the time we hit vanadium oxide, we have a metal. You can see from this plot of the lattice constants, we have a discontinuous volume contraction on going through the metal insulator transition. Of course, the free energy versus volume curve is different in the metallic and insulating states [THIRD PICTURE]. Incidentally, chromium monoxide and scandium monoxide don't exist; it's possible to show from the thermodynamic data that this is because they are unstable with respect to decomposition into, for example, chromium metal and the sesquioxide Cr2O3.

For purposes of illustration, I'm only going to be interested in the last four: MnO, NiO, CoO, and FeO, because they are the interesting ones that we have a problem with, but we'll mainly deal with nickel oxide.

Just by way of observation, these four materials aren't quite as cubic as the FIRST PICTURE suggests; in fact they undergo tiny distortions, different in each case [TABLE], which are induced by the magnetic interactions. For example, nickel oxide is very slightly rhombohedrally distorted: we take opposite corners of the cube and we pull such that the cubic angle becomes 90.2 degrees instead of 90. Now that's a kind of magnetostriction. CoO however undergoes a small tetragonal distortion (pulling on opposite faces). I mention this since it will be something interesting to try and calculate later. These are such tiny effects that if we can do that, we must be doing something right.