In order to do some electronic structure calculations, we need to choose a
Hamiltonian. For illustrative purposes, I will begin by making the
unconventional choice of discussing the Hartree-Fock (HF) Hamiltonian. For very
good reasons most solid-state calculations are done with density functional
theory, but we will initially consider HF since:
(1) the Hartree-Fock
Hamiltonian corresponds to a well-defined approximation in many-body theory so
if you wish you can imagine I'm doing just that.
(2) We can see precisely
the effect of ignoring electron correlation, because the HF Hamiltonian doesn't
include any.
(3) It will simplify the discussion, because it's possible to
isolate what I mean by each of the contributions. While DFT may generally give
better results because it includes correlation effects a lot of the physics is
hidden inside the approximate exchange-correlation functional, and it is less
easy to isolate the relevant pieces.
I'm going to start by defining precisely what I mean by each of the terms
in this Hamiltonian. This is obviously trivial but bear with me. So, we have a
bunch of single-particle orbitals with electrons in them. And we just work out
matrix elements involving these orbitals.
(a) ONE-ELECTRON TERMS
Here are a couple of one electron operators
representing the kinetic energy and and electron nuclear attraction. Remember
that in the models that Peter Littlewood was talking about, 'kinetic energy'
means something like 'the 3d band width'.
(b) COULOMB (HARTREE) INTERACTION
This is just the classical Coulomb
interaction between independent electrons . It is helpful to think of the
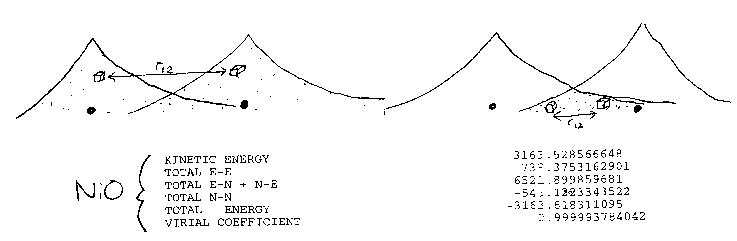
integration in terms of little boxes (volume elements) dr1
and dr2 separated by a distance r12 in a two
electron system like molecular hydrogen [SEE PICTURE ABOVE]. For a particular
choice of the two box positions the instantaneous energy of interaction in
atomic units is just 1/r12 from Coulomb's law. The total interaction
energy of the system is just the sum (i.e. integral) of these energies for all
possible positions of the boxes, with each contribution weighted by the square
of the single particle wave function of each particle (the probability of the
box being at that position). Note therefore that in the Hartree term the
position of one box is not considered to affect the position of the other
(independent electron approximation).
(c) EXCHANGE INTERACTION
The exchange interaction is of course not
actually an interaction - it is a correction to the Hartree term arising from
the constraint that the many-body wave function must be antisymmetric. With
this constraint the position of one little box affects the position of the
other. Now instead of having densities as the weighting factors in the
integral, we have overlap densities phi_a times phi_b. So you can think of it
this way; we're subtracting the interactions we just calculated in the Hartree
term for the case when the two little boxes are both in a region where the wave
functions of the electrons overlap. This happens only for electrons of the same
spin, so what we're doing is to correlate the motion of same spin electrons.
They effectively repel each other - this is sometime called Pauli repulsion and
we'll see that in action later on when we look at magnetism.
(d) CORRELATION ENERGY
This is a short range screening term to account
for the approximation we make in assuming that a given electron moves in the
average field for all the others. Feynmann actually has a good definition of
this in his statistical physics book - he calls it the stupidity energy.
For the perfectly good reason that it involves the same word, it is tempting to
equate this 'correlation' with the 'strong correlation' that we're currently
worried about. This is not correct. Strong correlation is actually something
like a big screened on-site Hartree-interaction, so it's actually some kind of
mixture of (b), (c) and (d), as we will see.
Peter Littlewood's definition of a strongly correlated material (see p.1 of
the notes for his course) was 'a material where the Coulomb interaction V is
greater than the kinetic energy T '. Note that this is not helpful when you
consider the energies of the whole system, as you can see from the above
breakdown into components of the total energy E in an electronic structure
calculation of the ground state of NiO [SEE TABLE]. The system approximately
obeys the virial theorem: E = -T = (1/2)V with a virial coefficient of 0.999994
(exact value 1.0). His statement is true only from the point of view of a model
system considering only the 3d Ni states, which is not so easy to calculate, so we
will have to look elsewhere for a precise definition that is relevant to
electronic structure theory.
Finally, for those who care, I mention a few computational details of the
calculations I will be talking about. All the calculations I show were done
under the assumption of periodic boundary conditions. Everything is done with
all-electron basis sets without using pseudopotentials, and the basis sets I
use are of high to very high quality (see basis set library link below).
Everything is spin polarized, so we will be using either unrestricted
Hartree-Fock (UHF) theory, or the LSDA as opposed to the LDA (local density
approximation) when we do density functional calculations.
|