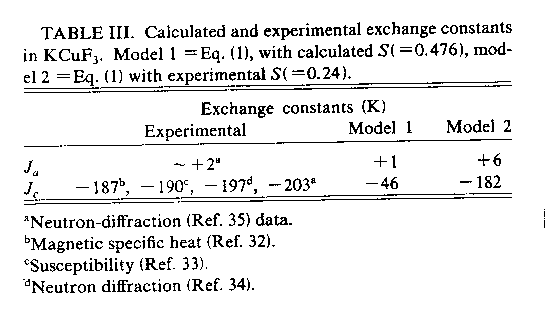|
Question: can we estimate experimentally-determined superexchange coupling
constants from these calculations? Answer: More or less. (WEBNOTE: and this has also been done recently by
people using fully-correlated quantum chemistry methods on small clusters..). Remember when we do HF calculations we have broken the spin symmetry.
There is no sense
in which the spin can be said to have a direction (the incorporation of 'non-collinear spins' with a vector magnetization density into electronic structure
theory is an active area of research). We only have the concept of
up and down spin - so this type of calculation corresponds most closely to an
Ising model of the spin. You can actually derive an Ising model type expression
which relates energy differences between magnetic states to the superexchange
coupling constant, in terms of the energy difference, the spin moment per site,
and a coordination number.. Now we don't expect this to work very well, but
what we have found is that the accuracy of this treatment depends on the
'magnetic dimensionality' of the system. In 3D you might get around 60% of the
true value, in 2D 50 %, in 1D about 40%. You expect that of course, because as
you lower the dimensionality fluctuations become more important. For example,
in KCuF3 we effectively have a one-dimensional magnet. In the real
system, the zero-point fluctuations in the spin direction will be very
important. What effect will they have? The main one will be to reduce the
on-site magnetic moment. So if I just plug in the Hartree-Fock on-site moment
into the Ising model expression, I get the numbers given in the above Table for
the exchange coupling constants along the different axes, which don't agree
very well with experiment, but at least we've reproduced the one
dimensionality. If you arbitrarily plug in the experimental on-site moment to
account for the zero point spin reduction, then we get essentially the right
answer. So at least you can see where the error lies. I should stress again
that this tends to work much better for higher dimensional magnetic systems,
and these results are in fact the worst that I've seen, in terms of
quantitative agreement..
|