21. KCuF₃ - III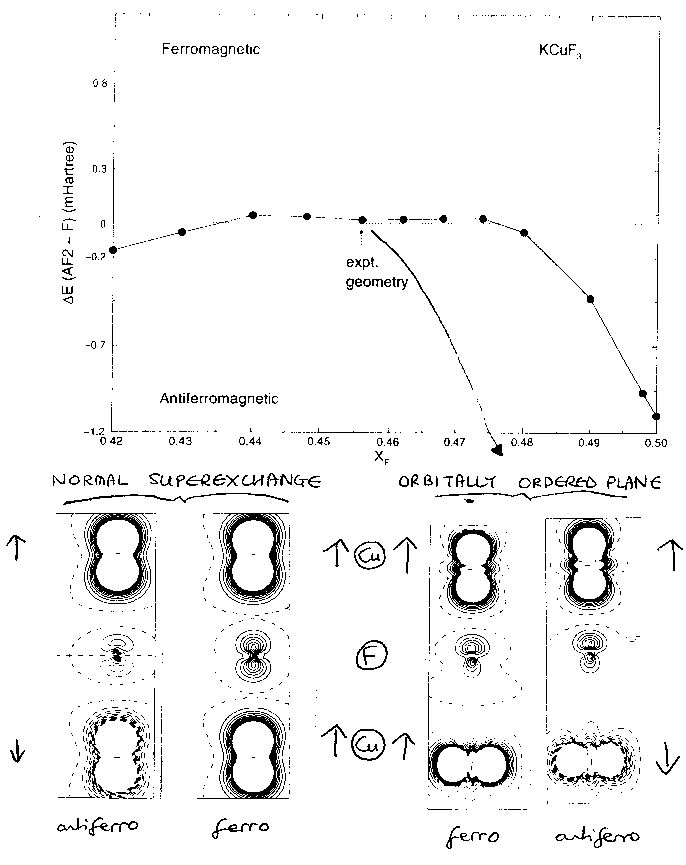

So can we explain the strange magnetic properties from these calculations? Yes - in the second diagram above I show some spin density plots. These are in extreme close up - the two on the left show the Cu-F-Cu bonds along the c axis, the two on the right are Cu-F-Cu bonds in the Jahn-Teller distorted plane perpendicular to the c axis. Continuous contours mean an excess of up-spin density, dotted lines an excess of down-spin density.

This is nice because it gives us a simple picture of what superexchange actually is. Remember I can flip the sign of the spin density of essentially any ion I want, by using different starting conditions for the SCF calculation. So by flipping the spins I can look at the converged spin density in the case where the Cu-F-Cu interaction is ferromagnetic or antiferromagnetic.

Look first at the two panels labelled 'NORMAL SUPEREXCHANGE' on the left above. You can see that there is a tiny spin polarization of the bridging 'non-magnetic' fluorine - if the plot were three dimensional then the peaks on the Cu ions (which are cut off in this picture) would be orders of magnitude taller than that on the F ion. In the ferromagnetic case, the 'contraction' of the up-spin density on the bridging fluorine is very large compared to that of the down-spin density. This is due to the large Pauli repulsion from the huge unpaired up spin density on the Cu ions. When I flip this spin to make the interaction antiferromagnetic, the system can reduce the exchange repulsion by shifting up-spin density towards the Cu with down-spin and vice versa. The 'closer average confinement' of up-spin electrons on the F ion means that the kinetic energy is much larger in the ferromagnetic case. This is easy to pick out looking at a breakdown of the total energy into components. So the arrangement of spin densities on the extreme left is the more stable, and superexchange contacts along the c-axis are antiferromagnetic..

What happens in the orbitally-ordered plane (the two panels on the right)? Well you can see that the unpaired spin density on the Cu ions is 'rotated out of the way' due to the orbital ordering, so that when I flip the spins, there is virtually no difference in the spin polarization of the F ion. Hence there is virtually no magnetic interaction between the one-dimensional magnetic strings going up the c-axis. In fact, experimentally the interaction in the orbitall ordered plane is very slightly ferromagnetic.

Luckily it also works out that way in the HF calculation. In the upper diagram on the overhead, I've plotted the total energy difference between the two panels on the right as a function of Jahn-Teller distortion. Where the plot is above the zero line the system is ferromagnetic. In the undistorted structure here (X_f=0.5), the magnetic interaction is antiferromagnetic, but not as much as up the c-axis, because there is still some residul orbital ordering caused by direct electrostatic interactions between the coppers (so the ordering is not completely lattice driven). However, as the crystal is Jahn-Teller distorted the orbital ordering becomes huge, and at the experimentally-observed value for the distortion the interaction in the orbitally-ordered plane becomes very slightly ferromagnetic.