5. NiO - what would we expect?

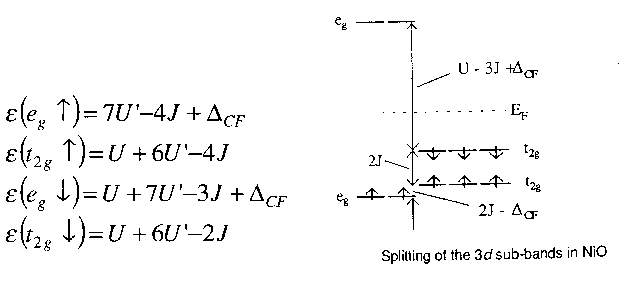
So, let's attempt to predict what we ought to get from a band theory calculation on NiO, in particular the expected form of the density of states. We will use a simple model and some nice parameters. The simplest version of the Hubbard model, whose Hamiltonian is shown above, is not really sufficient. In the 1960s and 70s, most of the theoretical effort was devoted to s electron models in which a Mott insulator was represented essentially as a lattice of hydrogen atoms. Now, this is a simplification which has obvious appeal, but it actually has a serious drawback. There was a general presumption that once the physics of the s electron model was understood, it would be simple and straightforward to extend the results to 3d systems. But what actually happened in the 1970s was that little effort was devoted to this second step. And that had the consequence that some crucial features, due specifically to the orbital degeneracy, werent understood or appreciated.

So we want to express the interactions in terms of some convenient phenomenological parameters. These are effective values which are supposed to incorporate all screening effects. Now, I want to include two other things beyond the basic s electron model, and those are (1) the exchange and (2) the fact that the effective on-site interaction between two d electrons will be different depending on whether they are both in the same d orbital or in different d orbitals.

Now a 3d band consists of 5 different orbitals, each of which may contain two electrons of opposite spin. So, I will define the on-site interactions U, U' and J as it says on the overhead. Obviously the U and J will be different for different pairs, so some averaging is implied here. Physically, this averaging just destroys Hund's second rule: the thing about coupling to maximum allowed L. That's quite acceptable for the 3d Mott insulators anyway, since L is strongly quenched by the crystal field. Now in NiO, the U parameter is much larger than any of the t values, so for now it makes sense just to ignore them. Finally we have a small crystal field splitting energy which splits the t_2g and e_g orbitals. Approximate experimental values for these parameters are also shown on the overhead.

Now consider an isolated Ni2+ ion in free space. Its basic physics is actually quite obvious: eight of the 3d orbitals will be full and two will be empty. Add a small cubic crystal field and we see that the two unoccupied orbitals will be two of the e_g orbitals. So I can now, very simply, write down expressions for the orbital energies for an electron in any of the d states. Now I stick the spectroscopic values in the expressions for the orbital energies and we have the energy level diagram which is shown on the overhead.

For example, if I am an up-spin t_2g electron, there is one down-spin electron in the same orbital as me, so I count one U. There are 6 other d electrons, so I count six U'. There are four electrons with the same spin as me, so I count -4 J. Result: U+6U'-4J.

You'll see that the up-spin e_g states actually live below the t_2g band, in contrast to the simple crystal field arguments I spoke about earlier. This is essentially due to the fact that the e_g orbitals are singly occupied. The unoccupied down-spin e_g states live well above the others essentially because an electron added into this state would feel the potential of 8 d electrons rather than 7 (this extra potential is essentially the 'Hubbard U').

This is the basic Mott-Hubbard picture: the potential is much higher for the empty orbitals than for the occupied orbitals, as we've just seen. It's fairly obvious that the same sort of physics must be occuring in NiO, which has a periodic lattice of Ni2+ ions. Now, that's not just an intuitive guess; there is strong and fairly direct experimental evidence for this physical picture. Consider the following overhead..