CASINO is a computer program system for performing quantum Monte Carlo (QMC) electronic structure calculations that has been developed by a group of reseachers initially working in the Theory of Condensed Matter group in the Cambridge University physics department, and their collaborators, over more than 20 years. It is capable of calculating incredibly accurate solutions to the Schrödinger equation of quantum mechanics for realistic systems built from atoms. This helps us understand and predict the nature of the Universe (as well as, you know, helping us to design drugs and superconductors and write grant applications). Other highly accurate methods are known that can do this of course, but what makes CASINO important is that – given a big enough computer – it can carry on doing this for systems containing hundreds or even thousands of atoms. These many atoms can form isolated giant molecules or groups of molecules, or they can be the repeating unit in an infinite crystal periodic in one, two, or three dimensions. Because of their inferior scaling with system size, competing methods of comparable accuracy generally struggle to handle more than a few tens of atoms.
CASINO is also important because QMC is one of the few methods genuinely capable of exploiting the power of modern computer hardware. The man in the street has probably noticed that computers stopped becoming faster because of increasing CPU frequency many years ago, and almost all modern performance improvements are down to increasing parallelism. The world’s fastest computers now have in excess of a million processor cores, and even your phone probably has at least four. You might expect that if you double the number of processing cores then the code would go twice as fast. Sadly for most popular methods in computational electronic structure – such as density functional theory – this stops being true very quickly as too much interprocessor communication is required. If you run the calculations on much more than a thousand cores, then they often start to slow down. Modern versions of CASINO, by contrast, have been shown to exhibit essentially perfect parallel efficiency when accumulating statistical averages on machines with hundreds of thousands of cores in all of its various modes of operation. The largest such CASINO calculations that we are aware of have been done are up to 524288 cores on Japan’s K-computer by Mike Towler – our good friend and colleague Ryo Maezono tells me the local sysadmins were ‘shocked‘. The following diagram shows the ideal parallel efficiency achieved on up to 120000 cores of JaguarPF (a now defunct Cray XT5 at Oak Ridge National Lab) with CASINO (the red curve is for an earlier version of CASINO). The second graph is the one for the K computer up to over half a million processor cores.
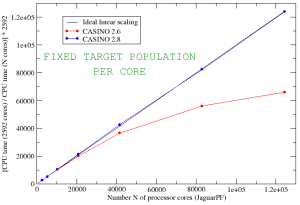
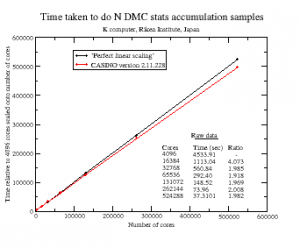
We would add similar data for common DFT codes but it usually wouldn’t be visible on this scale.
The QMC research program that culminated in CASINO as we know it today was begun in the early 1990s by Richard Needs, who had obtained inspiration from a short period working in the United States. He developed his initial ideas in collaboration with Guna Rajagopal and Matthew Foulkes and a number of early postdocs and students. Their initial test codes were gathered together and generalized into the first QMC program capable of treating any arbitrary system (named ‘CASINO’ after a suggestion from Paul Kent) by Mike Towler, who had arrived in Cambridge in late 1996. The first public version of CASINO was published in 1999. Absolutely fundamental improvements and generalizations of the code were made by Neil Drummond (from 2002) and Pablo López Ríos (from 2004). Needs, Towler, Drummond and López Ríos are now considered to be principal authors of the code, and all four of them continue to be at the heart of the project today. Sadly, CASINO was thrown off the Cambridge TCM group computer systems in September 2019 at the insistence of local computer management, despite Richard still working in the group, and as a result it is no longer possible to refer to it as the ‘Cambridge quantum Monte Carlo code’ .
Over the years, valuable additional contributions to the software base have been made by students, postdocs, and other people working in collaboration with us. A reasonably complete set would include Andrew Porter, Randy Hood, Andrew Williamson, Dario Alfè, Gavin Brown, Chris Pickard, Rene Gaudoin, Ben Wood, Zoltán Radnai, Andrea Ma, Ryo Maezono, John Trail, Paul Kent, Nick Hine, Alexander Badinski, Matthew Brown, Ken Esler, Andrew Morris, Norbert Nemec, Robert Lee, Priyanka Seth, Bohshiang Jong, Lucian Anton, Katie Schwarz, Pascal Bugnion, Jonathan Lloyd Williams, Elaheh Mostaani, Mike Deible, Vladimir Konjkov, Albert Defusco, Blazej Jaworowski, Marcin Szyniszewski, Ryan Hunt, David Thomas, Chung-Yuan Ren, Darryl Foo, Graham Spink, John Jumper, Katharina Doblhoff-Dier, Kayahan Saritas, Kevin Gasperich, Lars Schonenberg, Richard Dawes, Rodrigo Vargas-Hernandez, Thomas Whitehead and Tom Poole. (Please let me know if I’ve missed any out.)
CASINO is written entirely in standard-conforming Fortran 2003 using modern software design methods (yes, urban metrosexuals – Fortran is modern! Try writing this in Ruby on Rails or whatever is fashionable nowadays, and watch how quickly Fortran blows you out of the water). It’s supposed to be easy to use, easy to install, and easy to read and understand. It contains a self-documenting help system and comes with a helpful manual and examples. The distribution comes with a very large number of utilities and additional programs to help with analysis, running the code, and preparing the input. It is straightforward to mount CASINO across a variety of platforms (including workstations, weakly-linked clusters, massively parallel supercomputers, laptops and PCs. The Android app is in preparation). It uses standard MPI functions to work on parallel machines, but will work without it on single processors (having its own ‘fake’ serial MPI library). It can also make use of shared memory (Systems V, Posix, or nasty, buggy Blue Gene/Q Posix) whereby all MPI processes on, say, each 16-core node are able to access a common copy of selected large arrays, and OpenMP (which we use to implement a ‘second level’ of parallelization in which each MPI process can spawn a number of threads which parallelize over stuff like the number of electrons or orbitals).
For interested people who know what it means, a technical listing of CASINO’s scientific capabilities is as follows:
- Variational Monte Carlo. Wave function optimization achieved with variance minimization, accelerated variance minimization, energy minimization, and minimization of the mean absolute deviation of the set of local energies from the median.
- Fixed-node/fixed-phase diffusion Monte Carlo (pure or branching)
- Reptation Monte Carlo.
- Applicable to finite systems such as atoms and molecules and also to systems with periodic boundary conditions in 1, 2 or 3 dimensions (polymers, slabs/surfaces, crystalline solids) with any arbitrary crystal structure.
- Capable of using methods – called ‘linear scaling QMC’ in the literature – in which the time to move an electron scales linearly with the system size (but where the time taken to get the energy per simulation cell to a specified error bar in fact scales as the square of the system size. This is still very good compared to high accuracy quantum chemistry methods where the ‘gold standard’ methods scale as N^7).
- Can be used with different types of particles (electrons, positrons, ‘holes’, do-it–yourself particles with arbitrary mass and charge..) and combinations of such particles.
- Real or complex wave functions
- The code may use orbitals expanded in a variety of basis sets in the determinantal part of the many-electron trial wave function:
(1) Plane-waves (periodic systems) – even though inadvisable in QMC as it adds a factor of N to the scaling with system size.
(2) Blip functions, i.e., cubic splines on a regular grid (periodic and aperiodic systems) produced by a tranformation from plane-waves.
(3) s, sp, p, d, f or g Gaussian basis functions centred on atoms or elsewhere (aperiodic or periodic systems) with appropriate cusp corrections in the case of all-electron calculations.
(4) Slater functions centred on atoms
(5) Atoms or diatomic molecules with numerical orbitals interpolated from a grid. - Uses flexible Slater-Jastrow many-electron wave functions, where the Slater part may consist of multiple determinants.
- Support for ‘compressed determinant expansions’, which allow a large reduction in the computational cost of calculations using multi-determinants by using simple algebraic properties of determinants to combine the terms into fewer, more complex objects.
- Backflow correlations (also in inhomogeneous systems).
- Pairing wave functions and geminals .
- CASINO has established links to various other software packages via a generic interface for each basis set type. This allows us to use a variety of different techniques – such as Hartree-Fock or density functional theory – to generate trial wave functions – which are the starting point for QMC calculations. In certain cases (e.g. excited states) it is also desirable to generate multi-determinant trial wave functions via standard quantum chemistry methods such as CIS/CISD/TD-DFT/CASSCF methods. Thus, any system that can be treated with any of the programs listed below can in principle also be handled within QMC, and CASINO can usually be used to ‘make the answer better’.
Plane-waves/blips
For calculations with plane-waves or blip function basis sets we can use
(1) PWSCF (part of the Quantum Espresso package) – this has the most advanced built-in support and can even do blip transformations natively.
(2) ABINIT
(3) CASTEP
(4) MCEXX
(5) GP
Gaussians
With Gaussian basis sets we have used the following programs to calculate trial wave functions:
(6) CRYSTAL (95/98/03/06/09/14). DFT/HF for molecules and systems periodic in 1,2 or 3 dimensions.
(7) GAUSSIAN (94/98/03/09). Huge quantum chemistry package for molecules.
(8) GAMESS-US
(9) TURBOMOLE
Additional links with MOLPRO, CFOUR, and PSI4 are in development.
Slater
For calculations with Slater basis sets we use
(10) ADF
Numerical orbitals
Converters are provided for the numerical atomic HF code A2SP2K, and the diatomic code 2DHF. - Non-local pseudopotentials with s, p, d non-locality, and core polarization potentials. Possibility to use Casula non-local scheme.
- Computation of ground and excited state energies.
- Computation of forces on atoms in VMC or DMC (Gaussian basis sets only).
- Coupled DFT-DMC molecular dynamics calculations (with the PWSCF code).
- Computation of various expectation values such as pair correlation functions, density matrices, densities and spin densities, localization tensors, dipole moments, momentum density, and structure factors.
- Periodic Coulomb interactions computed either with standard Ewald methods or with our MPC (modified periodic Coulomb) interaction which is both faster than the Ewald method and exhibits smaller ‘Coulomb finite-size effects’. Twist averaging. Coulomb finite size effects also computable with alternative structure factor method.
- Spin-polarized calculations (e.g., of magnetic solids).
- Non-collinear spin systems (for a restricted set of cases
And apart from all that it’s just way cooler than any other QMC code, especially the one that Lucas wrote.
